邏輯代數中,用以描述邏輯關系的函數稱為邏輯函數。前面討論的與、或、非、與非、或非、異或都是邏輯函數。邏輯函數是從生活和生產實踐中抽象出來的,但是只有那些能明確地用“是”或“否”作出回答的事物,才能定義為邏輯函數。
1、邏輯函數的建立
例如,3個人表決一件事情,結果按“少數服從多數”的原則決定,試建立邏輯函數。
將實際問題中的邏輯關系表達為邏輯函數,需要以下3個步驟。
第一步:定義自變量和因變量。將3個人的意見設置為自變量A、B、C,并規定只能有同意或不同意兩種意見。將表決結果設置為因變量Y,顯然也只有通過或不通過兩種情況。
第二步:定義變量狀態的邏輯取值。對于自變量A、B、C,設:同意為邏輯“1”,不同意為邏輯“0”。對于因變量Y,設:表決通過為邏輯“1”,沒通過為邏輯“0”。
第三步:根據題意及上述規定列寫邏輯函數(真值表如表1所示)。
表1 真值表
| A | B | C | Y |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
由真值表可以看出,當自變量A、B、C取值確定后,因變量Y的值就完全確定了。所以,Y就是A、B、C的函數。A、B、C常稱為輸入邏輯變量,Y稱為輸出邏輯變量。
一般地說,若輸出邏輯變量A、B、C、…的取值確定以后,輸出邏輯變量Y的值也就唯一地確定了,就稱Y是A、B、C、…的邏輯函數,寫作
| (1) |
邏輯函數與普通代數中的函數相比較,有兩個突出的特點。
①邏輯變量和邏輯函數只能取兩個值0和1。
②函數和變量之間的關系是由“與”、“或”、“非”3種基本運算決定的。
|
2、邏輯函數的表示方法 |
邏輯函數通常有四種表示方法,即真值表、函數表達式、邏輯圖和卡諾圖。先介紹前3種表示方法,卡諾圖的方法在邏輯函數的化簡章節中詳細介紹。下面結合一個實例來講解。
例如,如圖1所示,有一個T形走廊,在相會處有一盞路燈,在進入走廊的A、B、C三地各有一個控制開關,都能獨立地進行控制。
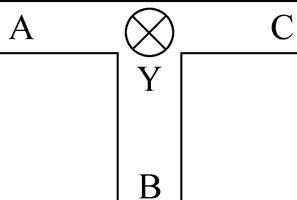 |
| 圖1 三地控制一燈示意圖 |
控制要求:
任意閉合一個開關,燈亮;
任意閉合兩個開關,燈滅;
3個開關同時閉合,燈亮。
要求列寫邏輯函數Y。
設A、B、C代表3個開關(輸入變量),開關閉合狀態為“1”,斷開狀態為“0”;燈亮Y(輸出變量)為“1”,燈滅“0”。
(1)真值表
真值表是將輸入邏輯變量的各種可能取值和相應的函數值排列在一起而組成的表格。按照上述邏輯要求,可以列出邏輯真值表(見表2)。www.tuo13886.net.cn
表2 三地控制一燈邏輯真值表
| A | B | C | Y |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
輸入變量的取值組合數隨著輸入變量個數不同而不同:兩個輸入變量的取值組合有4種;3個輸入變量的取值組合有8種;……;如果有n個輸入變量,則有2n種取值組合。為避免遺漏,各變量的取值組合應按照二進制遞增的次序排列。
從表2可以看出,用真值表表示邏輯函數有以下特點。
①直觀明了,輸入變量取值一旦確定后,即可在真值表查出相應的函數值。
②把一個實際的邏輯問題抽象成一個邏輯函數時,使用真值表是最方便的。所以,再設計邏輯電路時,總是先根據設計要求列出真值表。
③真值表的缺點是,當變量比較多,表比較大,顯得過于繁瑣。
(2)函數表達式
函數表達式就是由邏輯變量和“與”、“或”、“非”3種運算符所構成的表達式。邏輯函數表達式可根據真值表寫出,如表2所示。
方法:在真值表一次找出函數值等于1的變量取值組合,寫出與該取值組合對應的自變量乘積項。“1”寫成原變量,“0”寫成反變量。然后把這些乘積相加,就得到相應的函數表達式了。
根據表2所示邏輯真值表寫出邏輯函數表達式為
| (2) |
用邏輯函數表達式表示邏輯函數,便于研究邏輯電路,通過對邏輯函數式的化簡,可以簡化邏輯電路。缺點:邏輯函數式所表達式的邏輯關系不直觀。
(3)邏輯圖
邏輯圖就是由邏輯圖形符號及其之間的連線而構成的圖形。由函數表達式可以畫出其相應的邏輯圖。
方法:根據邏輯函數表達式中個邏輯變量運算的優先級順序畫出邏輯電路圖。
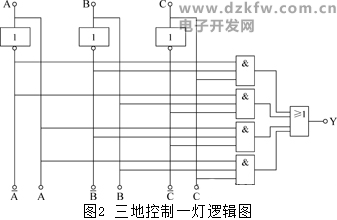
在邏輯函數表達式(2)中,優先級最高的是非運算,其次是與運算,最后是或運算。根據該優先級順序依次畫出邏輯圖(見圖2)。


 返回頂部
返回頂部 刷新頁面
刷新頁面 下到頁底
下到頁底