進位計數制

1、十進制

          

                                  

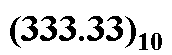
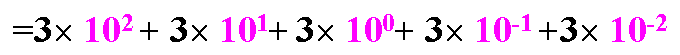
特點：1)基數10，逢十進一，即9+1=10

      2)有0-9十個數字符號和小數點，數碼K_i從0-9

      3)不同數位上的數具有不同的權值

      10ⁱ 10為數基 i表示相對小數點的位置

      4)任意一個十進制數，都可按其權位展成多項式的形式

         

            

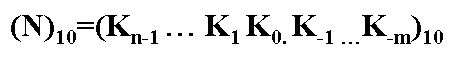
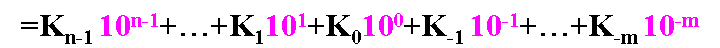
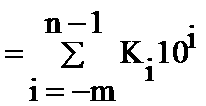
二進制

1)基數2，逢二進一，即1+1=10

2)有0-1兩個數字符號和小數點，數碼K_i從0-1

3)不同數位上的數具有不同的權值2ⁱ。

4)任意一個二進制數，都可按其權位展成多項式的形式

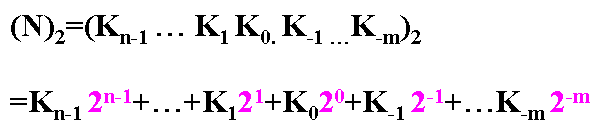
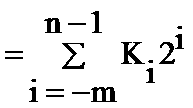
任意進制

1）基數R，逢R進一

2) 有R兩個數字符號和小數點，數碼K_i從0-R-1

3）不同數位上的數具有不同的權值R_i

4) 任意一個R進制數，都可按其權位展成多項式的形式

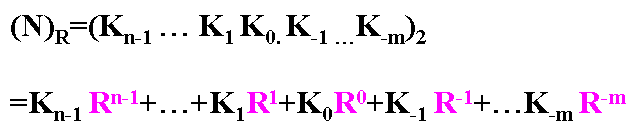
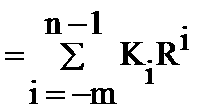
常用數制對照表

                  

數制轉換

十進制與非十進制間的轉換

十進制轉換成非十進制     非十進制轉換成十進制

非十進制間的轉換

二進制轉換成八、十六進制     八、十六進制轉換成二進制

十進制轉換成二進制

整數部分的轉換

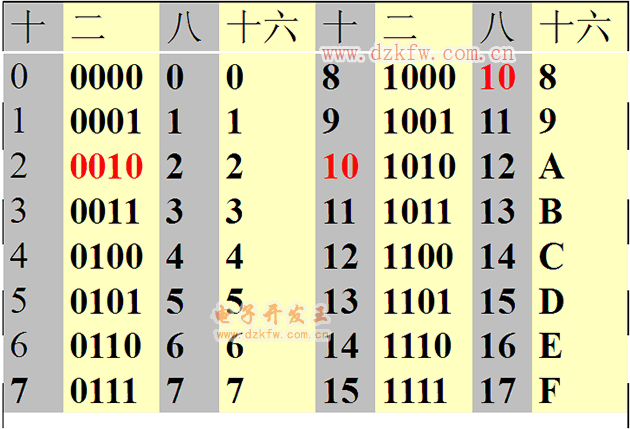
除基取余法：用目標數制的基數（R=2）去除十進制數，第一次相除所得余數為目的數的最低位 K₀，將所得商再除以基數，反復執行上述過程，直到商為“0”，所得余數為目的數的最高位K_n-1

例：(81)₁₀=(？)₂

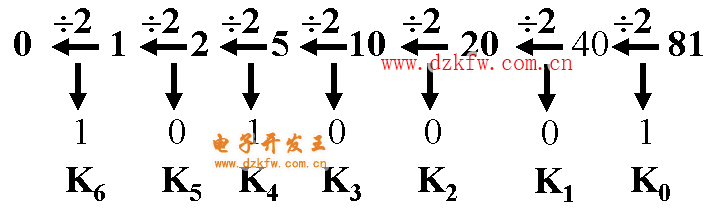
得:(81)₁₀=(1010001)₂

小數部分的轉換

乘基取整法：小數乘以目標數制的基數（R=2），第一次相乘結果的整數部分為目的數的最高位K-1，將其小數部分再乘基數依次記下整數部分，反復進行下去，直到小數部分為“0”，或滿足要求的精度為止(即根據設備字長限制，取有限位的近似值,如2-5，只要求到小數點后第五位)

例： （0.65）₁₀ =( ? )₂ 要求精度為小數五位。

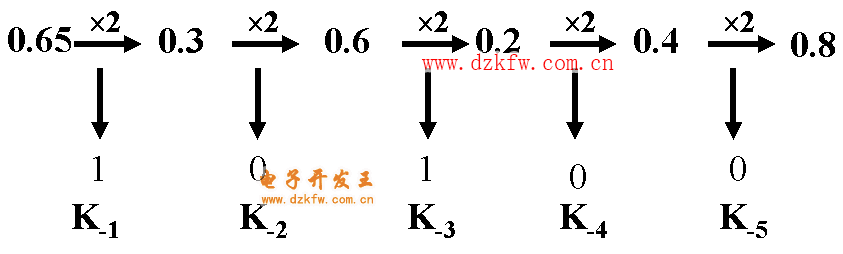
（0.65）₁₀ =( 0.10100 )₂

（81.65）₁₀ =( 1010001.10100 )₂

十進制二進制八、十六進制

非十進制轉成十進制

方法:將相應進制的數按權展成多項式，按十進制求和

例:

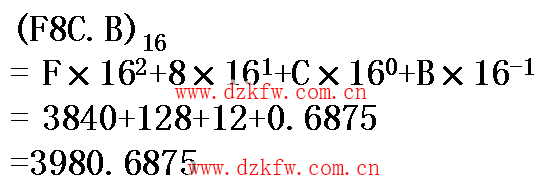
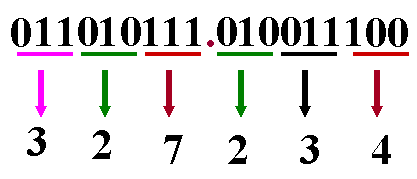
二進制與八進制間的轉換

從小數點開始，將二進制數的整數和小數部分每三位分為一組，不足三位的分別在整數的最高位前和小數的最低位后加“0”補足，然后每組用等值的八進制碼替代，即得目的數

例8: 11010111.0100111 B = 327.234 Q

以小數點為界

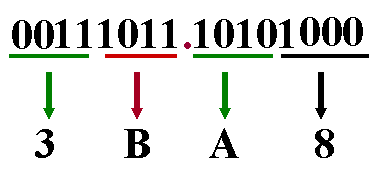
二進制與十六進制間的轉

從小數點開始，將二進制數的整數和小數部分每四位分為一組，不足四位的分別在整數的最高位前和小數的最低位后加“0”補足，然后每組用等值的十六進制碼替代，即得目的數

例9： 111011.10101 B = 3B.A8 H

以小數點為界

數值數據的表示

一、真值與機器數

真值：數符（+/-）+尾數（數值的絕對值）

機器數：符號（+/-）數碼化 最高位：“0”表示“+”“1”表示“-”

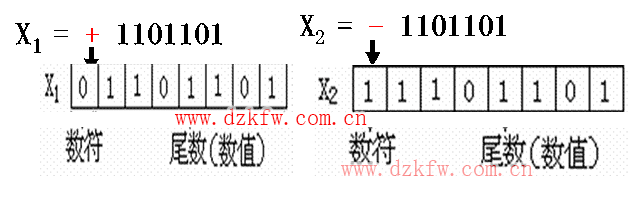
二、帶符號二進制數的代碼表示

1. 原碼[X]_原：符號位＋尾數部分（真值）

符號位最高位：“0”表示“+”“1”表示“-”

原碼的性質:

“0”有兩種表示形式[+00…0]_原 = 000…0 而 [-00…0]_原 = 100…0

數值范圍： +（2^n-1-1）≤[X]_原≤-（2^n-1-1）如n = 8，原碼范圍01111111～11111111，數值范圍為+127～-127

符號位后的尾數即為真值的數值

正數：尾數部分與真值形式相同

負數：尾數為真值數值部分按位取反

2. 反碼[X]_反：符號位+尾數部分

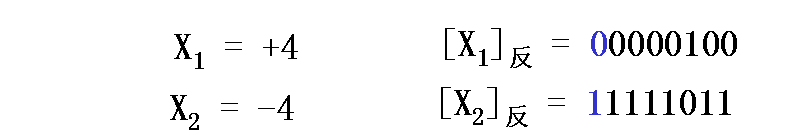
反碼的性質

“0”有兩種表示形式[+00…0]_反 = 000…0 而 [-00…0]_反 = 111…1

數值范圍： +（2^n-1-1）≤[X]_反≤-（2^n-1-1）如n = 8，反碼范圍01111111～10000000，數值范圍為+127～-127

符號位后的尾數是否為真值取決于符號位

3、補碼[X]_補：符號位+尾數部分

正數：尾數部分與真值同即[X]_補 = [X]_正

負數：尾數為真值數值部分按位取反加1即[X]_補 = [X]_反 + 1

補碼的性質：

0”有一種表示形式[+00…0]_補 = 000…0 而 [-00…0]_補 = 1 000…0

數值范圍： +(2^n-1-1）≤[X]_補≤-2^n-1如n = 8，補碼范圍01111111～10000000，數值范圍為+127～-128

符號位后的尾數并不表示真值大小用補碼進行運算時，兩數補碼之和等于兩數和之補碼，即[X1]_補+[X2]_補 = {X1+X2}_補（mod 2_n）

常用編碼

編碼:用一組二進制碼按一定規則排列起來以表示數字、符號等特定信息。

常用的編碼:自然二進制碼 格雷碼 二—十進制碼 奇偶檢驗碼 ASCII碼等。

（一）自然二進制碼及格雷碼

自然二進制碼:按自然數順序排列的二進制碼

            常用四位自然二進制碼，表示十進制數0--15，各位的權值依次為2³、2²、2¹、2⁰。

格雷碼:1.任意兩組相鄰碼之間只有一位不同。注：首尾兩個數碼即最小數0000和最大數1000之間也符合此特點，故它可稱為循環碼

       2.編碼還具有反射性，因此又可稱其為反射碼

（二）二—十進制BCD碼

有權碼:用四位二進制代碼對十進制數的各個數碼進行編碼。四位二進制數中的每一位都對應有固定的權

      有權碼表示十進制數符：D = b₃w₃ + b₂w₂ + b₁w₁ + b₀w₀ + c 偏權系數c = 0時為有權碼。

1.8421BCD（NBCD）碼

例：（276.8）₁₀ =（?）_NBCD

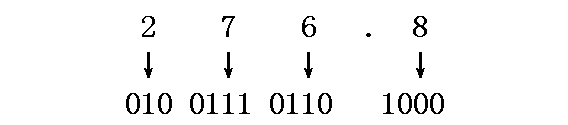
（276.8）₁₀ =（0010011101101000）_NBCD

2.其它有權碼:2421、5421、5211

無權碼

1 .余3碼:余3碼中有效的十組代碼為0011～1100代表十進制數0--9

2 .其它無權碼字符編碼ASCII碼：七位代碼表示128個字符 96個為圖形字符控制字符32個。