
邏輯代數(shù)的三個規(guī)則
1、代入規(guī)則
在任一邏輯等式中,如果將等式兩邊所有出現(xiàn)的某一變量都代之以一個邏輯函數(shù),則此等式仍然成立,這一規(guī)則稱之為代入規(guī)則。
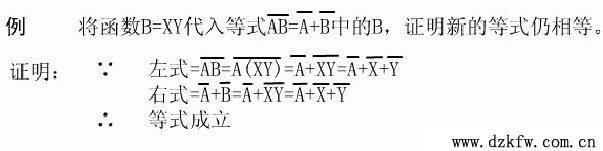
2、反演規(guī)則
已知一邏輯函數(shù)F,求其反函數(shù)時,只要將原函數(shù)F中所有的原變量變?yōu)榉醋兞浚醋兞孔優(yōu)樵兞浚弧埃弊優(yōu)椤啊ぁ?“·”變?yōu)椤埃保弧?”變?yōu)椤?”;“1”變?yōu)椤?”。這就是邏輯函數(shù)的反演規(guī)則。
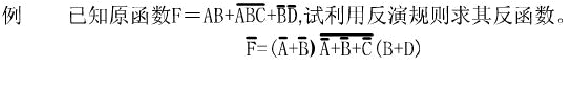
3、對偶規(guī)則
已知一邏輯函數(shù)F,只要將原函數(shù)F中所有的“+”變?yōu)椤啊ぁ?“·”變?yōu)椤埃保弧?”變?yōu)椤?”;“1”變?yōu)椤?”,而變量保持不變、原函數(shù)的運算先后順序保持不變,那么就可以得到一個新函數(shù),這新函數(shù)就是對偶函數(shù)F'。
其對偶與原函數(shù)具有如下特點:
1.原函數(shù)與對偶函數(shù)互為對偶函數(shù);
2.任兩個相等的函數(shù),其對偶函數(shù)也相等。這兩個特點即是邏輯函數(shù)的對偶規(guī)則。
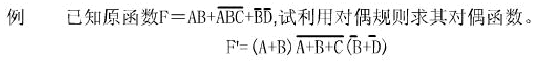
邏輯運算的常用公式



 返回頂部
返回頂部 刷新頁面
刷新頁面 下到頁底
下到頁底