化簡具有無關(guān)項的邏輯函數(shù)時，如果能合理利用這些無關(guān)項，一般都可得到更加簡單的化簡結(jié)果。

為達到此目的，加入的無關(guān)項應(yīng)與函數(shù)式中盡可能多的最小項（包含原有的最小項和已寫入的無關(guān)項）具有邏輯相鄰性。合并最小項時，究竟把卡諾圖上的×作為1（即認(rèn)為函數(shù)式中包含了這個最小項）還是作為0（即認(rèn)為函數(shù)式中不包含這個最小項）對待，應(yīng)以得到的相鄰最小項矩形組合最大、而且矩形組合數(shù)目最少為原則。

例1：化簡邏輯函數(shù)

，

給定其約束條件

解：如果不利用約束項，則Y已無可化簡。但適當(dāng)?shù)丶舆M一些約束項以后，可以得到

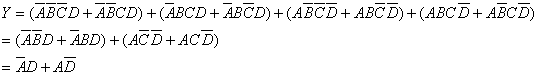
利用了約束項以后，使邏輯函數(shù)得以進一步化簡。但是代數(shù)法表示不夠直觀。從邏輯函數(shù)的卡諾圖上則表示得更清晰。

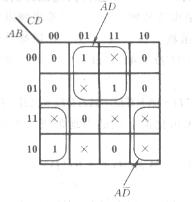
例2： 試化簡邏輯函數(shù)：

已知其約束條件為：

解：畫出函數(shù)Y的卡諾圖，

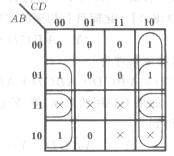
于是得到 ：