一、什么是格雷碼?
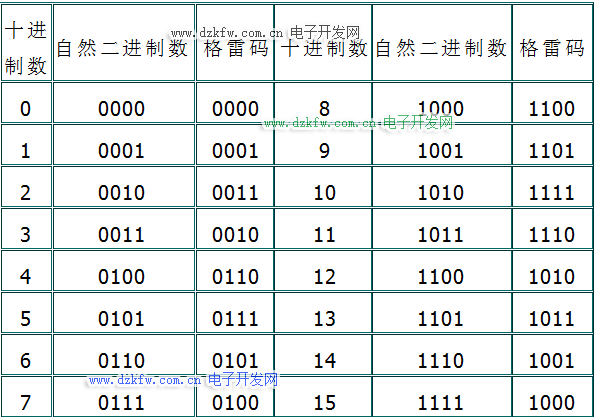
格雷碼,又叫循環(huán)二進(jìn)制碼或反射二進(jìn)制碼,格雷碼是我們在工程中常會遇到的一種編碼方式,它的基本的特點(diǎn)就是任意兩個相鄰的代碼只有一位二進(jìn)制數(shù)不同,這點(diǎn)在下面會詳細(xì)講解到。格雷碼的基本特點(diǎn)就是任意兩個相鄰的代碼只有一位二進(jìn)制數(shù)不同,這點(diǎn)很重要。常用的二進(jìn)制數(shù)與格雷碼間的轉(zhuǎn)換關(guān)系如下表:
二、二進(jìn)制格雷碼與自然二進(jìn)制碼的互換
1、二進(jìn)制碼轉(zhuǎn)換成二進(jìn)制格雷碼
二進(jìn)制碼轉(zhuǎn)換成二進(jìn)制格雷碼,其法則是保留二進(jìn)制碼的最高位作為格雷碼的最高位,而次高位格雷碼為二進(jìn)制碼的高位與次高位相異或,而格雷碼其余各位與次高位的求法相類似。

轉(zhuǎn)換代碼:
//根據(jù)二進(jìn)制轉(zhuǎn)換成格雷碼的法則,可以得到以下的代碼:
static unsigned int DecimaltoGray(unsigned int x)
{
return x^(x>>1);
}
//以上代碼實(shí)現(xiàn)了unsigned int型數(shù)據(jù)到格雷碼的轉(zhuǎn)換,最高可轉(zhuǎn)換32位自然二進(jìn)制碼,超出32位將溢出。
static int DecimaltoGray( int x)
{
return x^(x>>1);
}
//以上代碼實(shí)現(xiàn)了 int型數(shù)據(jù)到格雷碼的轉(zhuǎn)換,最高可轉(zhuǎn)換31位自然二進(jìn)制碼,超出31位將溢出。 2、二進(jìn)制格雷碼轉(zhuǎn)換成二進(jìn)制碼
二進(jìn)制格雷碼轉(zhuǎn)換成二進(jìn)制碼,其法則是保留格雷碼的最高位作為自然二進(jìn)制碼的最高位,而次高位自然二進(jìn)制碼為高位自然二進(jìn)制碼與次高位格雷碼相異或,而自然二進(jìn)制碼的其余各位與次高位自然二進(jìn)制碼的求法相類似。 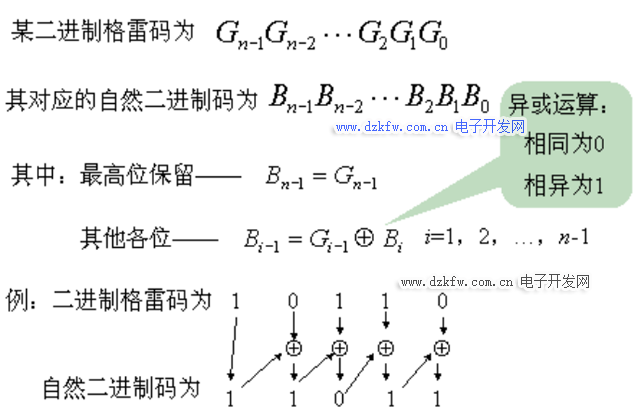
轉(zhuǎn)換代碼:
根據(jù)二進(jìn)制格雷碼轉(zhuǎn)換成自然二進(jìn)制碼的法則,可以得到以下的三種代碼方式:
static unsigned int GraytoDecimal(unsigned int x)
{
unsigned int y = x;
while(x>>=1)
y ^= x;
return y;
}
static unsigned int GraytoDecimal(unsigned int x)
{
x^=x>>16;
x^=x>>8;
x^=x>>4;
x^=X>>2;
x^=x^1;
return x;
}
static unsigned int GraytoDecimal(unsigned int x)
{
int i;
for(i=0;(1<<i)<sizeof(x)*8;i++)
{
x^=x>>(1<<i);
}
return x;
}
//以上代碼實(shí)現(xiàn)了unsigned int型數(shù)據(jù)到自然二進(jìn)制碼的轉(zhuǎn)換,最高可轉(zhuǎn)換32位格雷碼,
超出32位將溢出。將數(shù)據(jù)類型改為int型即可實(shí)現(xiàn)31位格雷碼轉(zhuǎn)換。


 返回頂部
返回頂部 刷新頁面
刷新頁面 下到頁底
下到頁底