1、線性性
【元件的線性性】當描述元件的特性方程為線性方程時,元件為線性元件,如線性電阻元件有![]() 的特性方程,線性受控源(CCVS)
的特性方程,線性受控源(CCVS)![]() 。
。
【線性電路】 除外,電路中的其他元件均為線性元件,這種電路稱為線性電路
【線性時不變電路】除獨立電源外,電路中其他元件均為線性元件,且是時不變元件,這種電路稱為線性時不變電路。
【電路的線性性】線性電路中,響應(電路中的任何電壓或電流)和激勵(獨立電壓源與獨立電流源)的關系為線性關系。線性關系體現為可加性和齊次性。
【齊次性】 在僅有一個獨立電源激勵的線性電路中,若將激勵增大K倍,響應也相應增大K倍,如圖4-1-1所示,如果![]() 激勵下的某個響應(電路中的任何電壓或電流)為
激勵下的某個響應(電路中的任何電壓或電流)為![]() ,則
,則![]() 激勵下的某個響應為
激勵下的某個響應為![]() 。
。

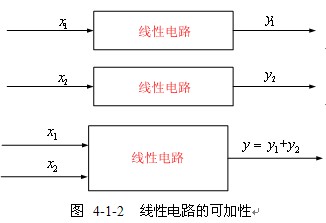
【可加性】 多個激勵共同作用引起的響應,等于每個激勵單獨作用所引起的響應之和。如圖4-1-2所示,如果![]() 激勵下的某個響應為
激勵下的某個響應為![]() ,
,![]() 激勵下的某個響應為
激勵下的某個響應為![]() ,則
,則![]() 和
和![]() 共同激勵下的響應為
共同激勵下的響應為![]() 。
。
2、疊加定理
【疊加定理】 對于任意線性電路,由多個獨立電源共同作用所引起的響應等于這些獨立電源分別單獨作用時所引起的響應的代數和。疊加定理是線性電路的線性性質的體現。
【例4-1-1】 應用疊加定理計算圖4-1-3(a)中電流![]() 和電壓
和電壓![]() 。
。
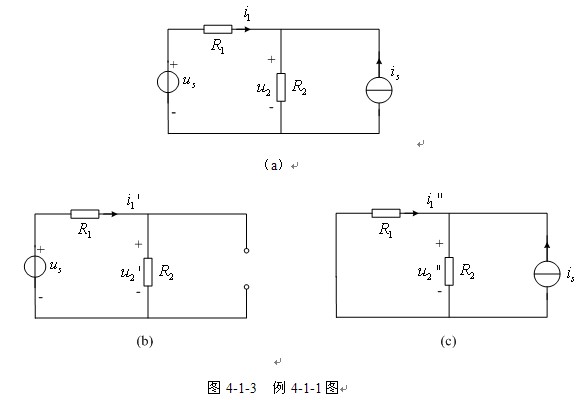
解 圖4-1-3(a)所示電路有一個獨立電壓源和一個獨立電流源,兩個電源共同作用下的響應可以由結點分析方程求得。即
![]()
解得 ![]()
則電流![]() 為
為 ![]()
通過疊加定理分析。獨立電源分別單獨作用的電路如圖4-1-3(b)、(c)所示。電壓源![]() 單獨作用電路如圖4-1-4(b)所示,有
單獨作用電路如圖4-1-4(b)所示,有
![]() ,
,![]()
電流源![]() 單獨作用電路如圖4-1-3(c)所示,有
單獨作用電路如圖4-1-3(c)所示,有
![]() ,
,![]()
根據疊加定理
![]()
![]()
可見,兩電源共同作用的響應是兩電源單獨作用時響應之和。本例的結果證明了疊加定理的結論。
【例4-1-2】 應用疊加定理計算圖4-1-4(a)所示電路中的電壓u。并確定40Ω電阻消耗的功率。
解 本例若采用結點分析法,要建立兩個結點方程,求解方程工作量不大,應該優先選擇結點分析。用疊加定理分析時,獨立電源分別作用的電路如圖4-1-4(b)、(c)、(d)所示,三個電路的分析均可以采用分壓、分流關系實現,計算工作量也不太大,可以選擇疊加定理來分析。根據疊加定理,![]() 。
。
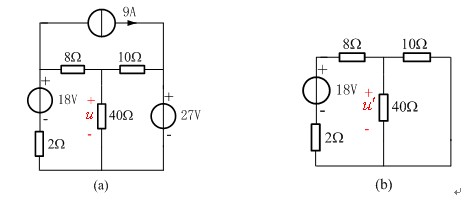
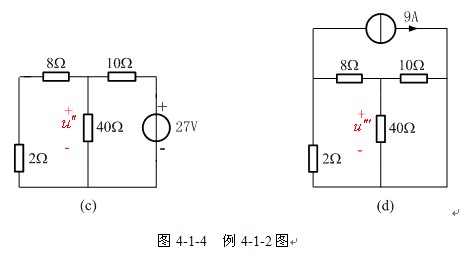
按照電阻串聯、并聯和分壓關系,不難得到
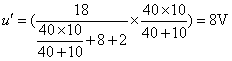
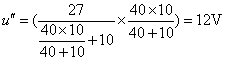
圖(d)中, 10Ω和40Ω電阻并聯,結果為8Ω電阻,兩個8Ω電阻串聯,再和2Ω并聯,由分流關系不難得到
![]()
因此 ![]()
功率 ![]()
但![]() ,即功率不符合疊加定理。
,即功率不符合疊加定理。
【例4-1-3】電路如圖4-1-5(a)所示,試用疊加定理求受控電源端電壓U及其提供的功率。
解 本例最簡單分析方法應該是結點法,為了說明受控電源在疊加定理應用時的處理方法,在此用疊加定理分析。用疊加定理分析含受控電源電路時,受控電源保留在獨立電源單獨作用的各電路之中。電壓源和電流源分別單獨作用的電路如圖4-1-5(b)和(c)所示。
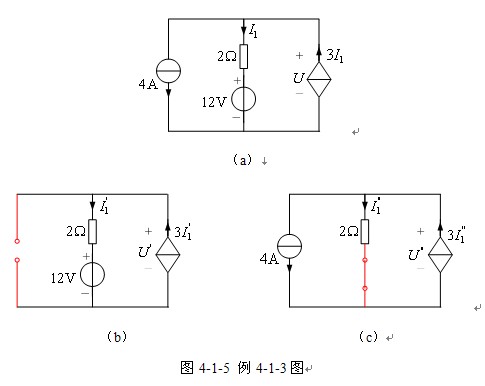
圖4-1-5(b)中,由KCL和KVL分別得到
![]()
![]()
解得 ![]()
![]()
圖 4-1-6(c)中,由KCL和KVL分別得到
![]()
![]()
解得 ![]()
![]()
當兩電源共同作用時, ![]()
![]()
受控電源提供的功率為 ![]()
【疊加定理應用注意事項】
1. 疊加定理僅適用于線性電路。
2. 應用疊加定理分析含受控源電路時,通常不把受控源單獨作用于電路,而把受控源作為電阻元件一樣對待,當某一獨立電源單獨作用時,受控源保留在電路中。
3. 疊加時應注意各響應分量的參考方向與原來的響應變量方向是否一致,方向一致則響應分量前應取“+”號,不一致則響應分量前應取“-”號。


 返回頂部
返回頂部 刷新頁面
刷新頁面 下到頁底
下到頁底