1．齊性定理
　　齊性定理：在只有一個激勵作用的線性電路中，設(shè)任一響應為，記作，若將該激勵乘以常數(shù)K，則對應的響應也等于原來響應乘以同一常數(shù)， 即。

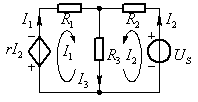
圖1 齊性定理示例

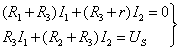　　　　　　(1)

　　當電壓源電壓改為時，設(shè)回路電流為，同樣可以列得回路電流方程：

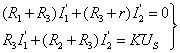　　　　　　(2)

　　另外，如將式(1)各項乘以，方程仍成立，此時得

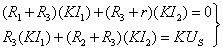　　　　(3)

　　方程(2)與(3)是兩個系數(shù)相同的線性方程組，所以有

，

　　即回路電流等于原來的倍。電路中其它響應均可通過回路電流的線性組合而得，所以它們的量值也同樣變?yōu)樵瓉淼?IMG src="/jichu/UploadFiles_6678/201911/20191111212153731.gif" width=17 height=17>倍。
　　例題1：圖示電路中電阻。(1)若使 I0 = 1A，求 US的值。(2)若 US = 66V，求各支路電流。

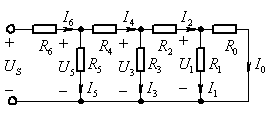
圖2 例題1

　　解： (1)根據(jù)KVL、KCL及歐姆定律，由已知電流依次遞推可以求出其它支路電流：

,,
,,

　　故所需電源電壓為：

　　(2) 此時相當于將電壓源乘以常數(shù)，根據(jù)齊性定理，各支路電流均變?yōu)樵瓉砹恐档?EM>K倍，即

，，，
，，。

　　2．疊加定理
　　疊加定理：在線性電路中，由幾個獨立電源共同作用產(chǎn)生的響應等于各個獨立電源單獨作用時產(chǎn)生相應響應的代數(shù)疊加。

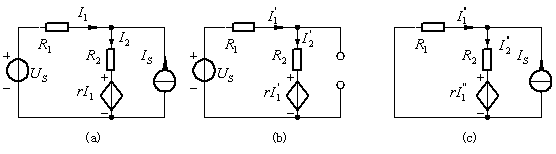
圖3 疊加定理示例

　　解：圖(a)電路：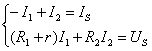　　
　　圖(b)電路：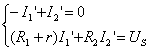　　
　　圖(c)電路：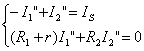　　
　　將上面兩個方程等號兩側(cè)對應項相加，得

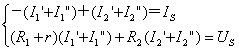
　　注：1、功率與獨立電源的源電壓和源電流不是線性關(guān)系，所以功率不能直接用疊加關(guān)系來計算。
　　2、線性直流電路的任一響應都是該電路中獨立電源的線性組合，即

　　例題2： 圖4(a)電路，用疊加定理計算電壓U。

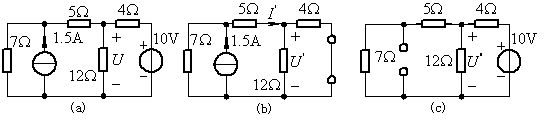
圖4　　例題2

　　解： (1)先使獨立電流源單獨作用，電壓源用短路代替，得圖(b)，計算其中電壓。利用電阻的串、并聯(lián)等效及分流公式得

　　(2)再使獨立電壓源單獨作用，電流源用開路代替，得圖(c)，計算其中電壓。

　　(3)根據(jù)疊加定理得待求電壓

　　例題3：圖示電路，已知當時，電壓。求當，其它條件不變時電壓U的值。

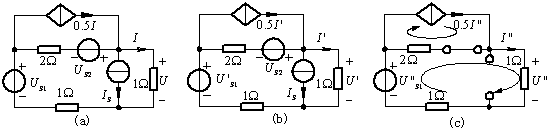
圖5　例題3

　　解：根據(jù)已知條件，將電壓源分解成。再利用疊加定理，將圖(a)電源的作用情況分解成圖(b)和圖(c)。在圖(b)中，所以；圖(c)中，只有單獨作用，對其列回路電流法方程可得

　　解得

，　

　　故題中所求電壓