零狀態是零原始狀態的簡稱。電路在零原始狀態下，僅由輸入激勵產生的響應稱為零狀態響應（ zero-state response ）。

    電路在單位階躍電壓或單位階躍電流激勵下的零狀態響應稱為單位階躍響 應 (unit-step response), 簡稱階躍響應 (step response) 。

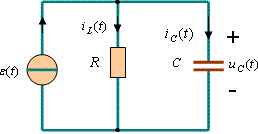    圖1 表示由單位階躍電流激勵的 RC 并聯電路。圖中ε（ t ）為單位階躍電流。當 t<0 時電路無輸入激勵， ；當 t>0 時，電流源向電路提供1A 的恒定電流。這時，電路中的任一響應( 電流或電壓 ) 僅僅是由單位階躍電流激勵產生的，即為電路的 的RC 并聯電路

    當 t=0 時，由于電容電流是有限值，電容電壓不能跳變，故 uc(0 + )= uc(0 - )=0， iR (0 + )=uc（0 +） /R=0 ，ic(0 + )=1A 。即

此時電容的充電電流等于電流源的電流。隨著充電過程的進行，電容電壓將從零開始逐漸升高，電阻中的電流也將從零開始逐漸增大，但電流源輸出的電流 ( 1A )卻保持不變，因此，電容電流必將逐步減小。當電容充電結束后， ，電流源的全部電流通過電阻。

    為了研究上述 RC 并聯電路的階躍響應，首先根據電路的基本約束關系建 立電路方程

              

或                          （1 ）

當 t 〉 0 時，式（ 1 ）變為

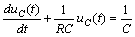                               （ 2 ）

    此即為 t>0 時電路的輸入 - 輸出方程，它是一個一階常系數線性非齊次微分方程。

    令式（ 2 ）的右端等于零，得齊次微分方程 為

                          

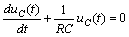
于是可得階躍響應電壓的自由分量為       

    由于電路的激勵函數在 t>0 時是一個常數，可設階躍響應電壓的強制分量 為一常數 K ，即           將此式代入非齊次微分方程式（ 2 ），得到

                          

  于是有                   K=R

強制分量                   

因此式（2 ）的通解為 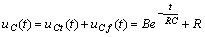     （ 5 ）

  由式 （5 ）令 ，并代入初始條件 ，可得

                               B+R=0

從而解得積分常數               B=-R

    將積分常數代入式（ 5 ），并將該式右端乘以單位階躍函數 ，便得到電路的階躍響應電壓為                   

                  

或                   

    階躍響應 的強制分量 在 t 〉 0 的區間內是一個常量， 因此， 又被稱為階躍響應 的穩態分量 (steady-state component) ，或稱穩態響應 (steaty-state response) 。線性電路對周期性激勵的強迫響應雖不是常量 ( 而是周期量 ) ，也稱為穩態響應。

    階躍響應 的自由分量 隨時間的增長按指數規律衰減，衰減的 決慢決定于電路的時間常數τ =RC ，當經過 4 τ —5 τ的時間后，即可認為 已消失。因此，階躍響應 的自由分量又被稱為暫態分量 (transient component) ，或稱暫態響應 ( transient response) 。當暫態分量衰減完后，階躍響應即等于其穩態分量。顯然，這就是電路中的電容在充電結束后( ) 具有的電壓。

    但須注意，暫態響應不一定等于自然響應，穩態響應不一定等于強迫響應。 如果激勵函數是隨時間的增長而衰減的 ( 例如指數脈沖 ) ，則受激勵函數約束的強迫響應也將隨時間的增長而衰減，它與激勵同時存在，同時消逝。這時穩態響應等于零，自然響應和強迫響應一并組成暫態響應。

    在暫態響應存在的時間內，電路的工作狀態稱為暫態 ( 或瞬變狀態 ) 。暫態響應衰減完以后，電路的工作狀態稱為穩定狀態 ( 簡稱穩態 ) 。圖1 所示電路在經過 4 τ -5 τ的時間后、即可認為進入穩定狀態，此時電路的響應即為穩態響應。

    電阻電流和電容電流可根據歐姆定律和基爾霍夫電流定律分別表示為

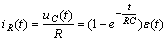
    階躍響應 、 、 的函數曲線分別描繪在圖2 中。由此 可見， 與 都是從它們的初始值開始，隨時間的增長按指數規律單調地上升，而 則是從它的初始值開始隨時間的增長按同一指數規律衰減，約經 4 τ —5 τ的時間后，它們分別等于各自的穩態分量 ( 電容電流的穩態分量為零 ) 。但電容電流在 t=0 時，由 跳變到 。

             

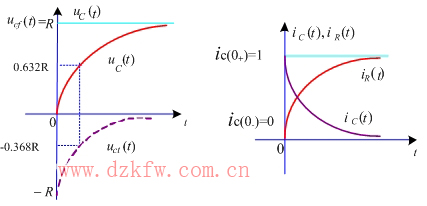
     （a）電容電壓及其穩態分量與暫態分量 （b）電流曲線

                    圖2 RC并聯電路的階躍響應曲線

    根據以上所得結果，不難看出，一階電路對階躍激勵的零狀態響應是激勵的線性函數。事實上，零狀態響應是電路在零原始狀態下僅由輸人激勵產生的響應，因而自然是激勵的線性函數。這對于線性電路而官，具有普遍意義。

    上面討論了一階電路的階躍響應。如果作用于同一電路的激勵函數是移位的單位階躍函數 ，則因電路參數不隨時間變化，電路的輸山響應與輸入激勵施加于電路的時刻無關，響應函數的曲線應與階躍響應曲線完全相同，僅僅在時間上延遲 ；這就是所謂電路的非時變性。例如圖1 所示 RC 并聯電路的階躍響應電壓 [ 式〔 6)] 為    

    激勵函數 與響應 的曲線示于圖 6(a) 與圖 6(b) 中。根據以上分析可得移位的單位階躍電流激勵 作用于同一電路的零狀態

響應電壓為

                

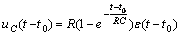
    與 的曲線示于圖 6(c) 與圖 6(d) 中。

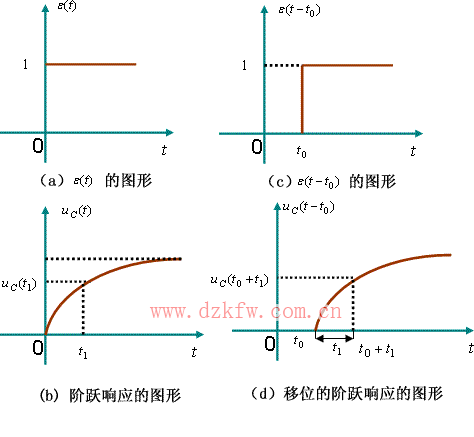
圖6 電路的非時變性的應用示例