第 4 節 一階電路的零狀態響應
零狀態響應:儲能元件的初始狀態為零,僅由外加激勵作用所產生的響應,稱為零狀態響應( zero-state response )。
一、 RC 電路的零狀態響應
圖 5.4-1 所示 RC 電路,開關閉合之前電路已處于穩態,且電容中無儲能,即 ![]() 。
。 ![]() 時開關閉合,討論
時開關閉合,討論 ![]() 時響應的變化規律。
時響應的變化規律。
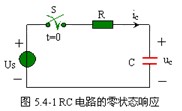
t=0 時開關閉合,則由換路定則得![]()
這時直流電壓源 Us 與 R 、 C 構成回路,由 KVL 得![]()
這是一階非齊次微分方程,它的解由對應的齊次微分方程的通解和非齊次微分方程的特解組成。采用常數變易法來解,得 RC 電路的零狀態響應為
![]()
![]()
![]()
![]()
當 t →∞時,電路已達到新的穩態,電容又相當于開路,則![]() ,
, ![]()
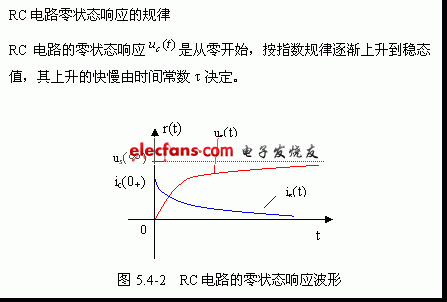
因此,電容電壓的零狀態響應為![]()
式中, ![]() 為 RC 電路的時間常數。
為 RC 電路的時間常數。
二、 RL 電路的零狀態響應
圖 5.4-3 所示電路, ![]() 時開關 S 處于閉合狀態,電感的初始狀態
時開關 S 處于閉合狀態,電感的初始狀態 ![]() ,
, ![]() 時開關打開。討論開關打開后響應的變化規律。
時開關打開。討論開關打開后響應的變化規律。
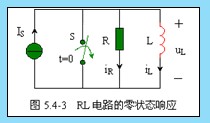
t=0 時,開關 S 打開,直流電流源 Is 開始對電感充電,這時![]()
這也是一階非齊次微分方程,解得
![]()
![]()
![]()
![]()
式中, ![]() 為 RL 電路的時間常數。當 t →∞時,這時電路已達到新的穩態,電感相當于短路。
為 RL 電路的時間常數。當 t →∞時,這時電路已達到新的穩態,電感相當于短路。
![]() ,
, ![]()
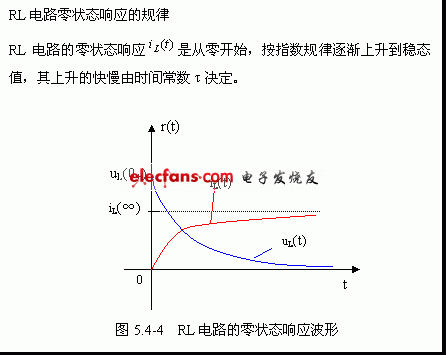
因此,電感電流的零狀態響應為![]()
三、一階電路零狀態響應的計算
計算步驟
1 、求 t →∞時的穩態值。
對于 RC 電路,求 ![]() ;對于 RL 電路,求
;對于 RL 電路,求 ![]() 。
。
2 、求電路的時間常數τ。
對于 RC 電路, ![]() ,對于 RL 電路,
,對于 RL 電路, ![]() 。其中, R 為從電容 C 或電感 L 兩端看進去的戴維南等效電阻。
。其中, R 為從電容 C 或電感 L 兩端看進去的戴維南等效電阻。
3 、求出零狀態響應
RC 電路: ![]()
![]()
RL 電路: ![]()
![]()
4 、如需求其它響應,再根據已求得的 ![]() 或
或 ![]() 去求解。
去求解。
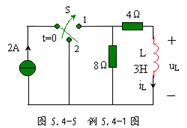
例 5.4-1 圖 5.4-5 所示電路,已知 ![]() 時開關 S 處于位置 2 ,且電感中無儲能, t=0 時開關 S 撥到位置 1 ,求
時開關 S 處于位置 2 ,且電感中無儲能, t=0 時開關 S 撥到位置 1 ,求 ![]() 時的
時的 ![]() ,
, ![]() 。
。
解:電感的初始儲能為 0 ,則 ![]()
電路換路后, t →∞時,電路進入新的穩態,電感又相當于短路,則![]()
換路后,從電感兩端看進去的等效電阻是 4 Ω和 8 Ω兩個電阻串聯,即R=4 + 8=12 Ω
所以,時間常數為![]()
因此,電路的零狀態響應為
![]()
![]()
![]()
![]()


 返回頂部
返回頂部 刷新頁面
刷新頁面 下到頁底
下到頁底