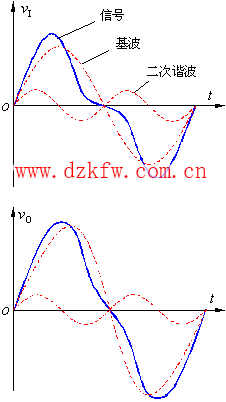
圖1
從信號的頻譜一節的討論可知,理論上許多非正弦信號的頻譜范圍都延伸到無窮大,而放大電路的帶寬卻是有限的,并且相頻響應也不能保持常數。例如圖1中輸入信號由基波和二次諧波組成,如果受放大電路帶寬所限制,基波增益較大,而二次諧波增益較小,于是輸出電壓波形產生了失真,這種由于放大電路對不同頻率信號的增益不同,產生的失真叫作幅度失真。
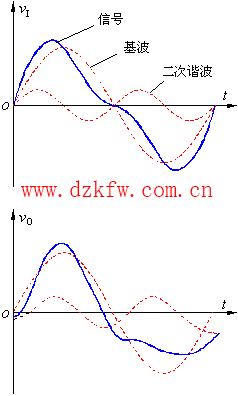 |
同樣,當放大電路對不同頻率的信號產生的相移不同時也要產生失真,稱為相位失真,在圖2中,如果放大后的二次諧波滯后了一個相角,輸出電壓也會變形。由傅里葉級數或傅里葉反變換也可反映出,無論頻譜函數還是相位譜函數發生變化,相應的時間函數波形都會由此而失真。幅度失真和相位失真總稱為頻率失真,它們都是由于線性電抗元件所引起的,所以又稱為線性失真,以區別于因為元器件特性的非線性造成的非線性失真。
為使信號的頻率失真限制在容許的程度之內,則要求設計放大電路時正確估計信號的有效帶寬(即包含信號主要能量或信息的頻譜寬度),以使放大電路帶寬與信號帶寬相匹配。放大電路帶寬過寬,往往造成噪聲電平升高或生產成本增加。
上述音響系統放大電路帶寬定在20Hz~20kHz,這與人類聽覺的生理功能相匹配。由于人耳對聲頻信號的相位變化不敏感,所以不過多考慮放大電路的相頻響應特性。但在有些情況下,特別是對信號的波形形狀有嚴格要求的場合,確定放大電路的帶寬還須兼顧其相頻響應特性。






 返回頂部
返回頂部 刷新頁面
刷新頁面 下到頁底
下到頁底