根據第一章中介紹的圖論知識可知,實際電路結構可用一個有向圖來具體描述。如某一電路的有向圖如圖7-2-1所示,把有向圖各節點和支路編號,然后依次把各支路與相應連接點的連接信息用數字形式記憶下來。根據這些信息可完整描述電路的聯接關系,若把這些信息輸入計算機,則計算機就會根據這些信息自動識別電路關系,并應用基爾霍夫定律建立相應的電路方程,進行相應的運算。
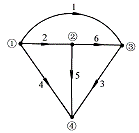
圖 7-2-1
電路中支路與節點的連接關系可用關聯矩陣來描述。設電路的節點數為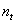 ,支路數為b。依次給節點和支路編號(節點編號用一圓圈加以區別),然后把有向圖用一個
,支路數為b。依次給節點和支路編號(節點編號用一圓圈加以區別),然后把有向圖用一個![]() 階矩陣來表示,記為
階矩陣來表示,記為![]() 。矩陣的行對應于有向圖的節點,矩陣的列對應于網絡的支路。
。矩陣的行對應于有向圖的節點,矩陣的列對應于網絡的支路。![]() 中的元素
中的元素![]() 作如下定義:
作如下定義:
 (7-2-1)
(7-2-1)
式中,![]() 稱為電路的節點—支路關聯矩陣。例如對于圖7-2-1所示的電路,可寫出關聯矩陣為:
稱為電路的節點—支路關聯矩陣。例如對于圖7-2-1所示的電路,可寫出關聯矩陣為:

關聯矩陣的每一列對應于一條支路,每一支路必連接于二個節點,且方向為一進一出。因此![]() 的每一列中只包含二個非零元素+1和-1,如上面關聯矩陣所示。如果把所有行的元素按列相加,則得到全零的行,因此矩陣
的每一列中只包含二個非零元素+1和-1,如上面關聯矩陣所示。如果把所有行的元素按列相加,則得到全零的行,因此矩陣![]() 的行不是彼此獨立的。對于
的行不是彼此獨立的。對于![]() 中任一行元素可以通過把除該行以外的所有行相加并變號而獲得。
中任一行元素可以通過把除該行以外的所有行相加并變號而獲得。
如果把![]() 的任一行劃去,剩下的矩陣為
的任一行劃去,剩下的矩陣為![]() 階矩陣
階矩陣![]() ,記作A。由上分析可知,用該新矩陣A來代替
,記作A。由上分析可知,用該新矩陣A來代替![]() 同樣能充分描述有向圖的連接關系,矩陣A稱為降價關聯矩陣,劃去的行對應的節點即為參考節點,上圖中若以節點④為參考點,則其降價關聯矩陣為
同樣能充分描述有向圖的連接關系,矩陣A稱為降價關聯矩陣,劃去的行對應的節點即為參考節點,上圖中若以節點④為參考點,則其降價關聯矩陣為

在實際應用中通常采用降價關聯矩陣形式,因此在一般敘述中往往略去“降價”二字。關聯矩陣可由給定的網絡有向圖得出,同樣當給定關聯矩陣A后也可推導出它所代表的有向圖。
關聯矩陣A的每一行是相互獨立的,每行之間是線性無關的,A的秩等于矩陣的行數![]() 。實際上由A的元素
。實際上由A的元素![]() 的定義可知,關聯矩陣的每一行反映了該節點的電流平衡關系式。A中線性獨立的n行代表了網絡中
的定義可知,關聯矩陣的每一行反映了該節點的電流平衡關系式。A中線性獨立的n行代表了網絡中![]() 個節點的電流平衡關系。
個節點的電流平衡關系。
下面分析關聯矩陣A與支路電流,支路電壓,節點電位之間的關系。設網絡各支路電流為![]() ,支路電流方向與有向圖支路方向一致,用矩陣形式表示的支路電流列向量為
,支路電流方向與有向圖支路方向一致,用矩陣形式表示的支路電流列向量為![]() 。
。
若用關聯矩陣A![]() 左乘支路電流列向量i,可得一n行的列向量矩陣。由關聯矩陣的定義可知,該列向量中每一行的元素之和恰為離開該節點的支路電流與流入該節點的支路電流之代數和,且離開節點時電流為正,流入節點時電流為負。由基爾霍夫節點電流定律可知,節點電流代數和恒為零。因此可得A左乘i后其值為零向量,即有:
左乘支路電流列向量i,可得一n行的列向量矩陣。由關聯矩陣的定義可知,該列向量中每一行的元素之和恰為離開該節點的支路電流與流入該節點的支路電流之代數和,且離開節點時電流為正,流入節點時電流為負。由基爾霍夫節點電流定律可知,節點電流代數和恒為零。因此可得A左乘i后其值為零向量,即有:
![]() (7-2-2)
(7-2-2)
該式反映了網絡各節點的電流平衡關系,稱為矩陣形式的基爾霍夫電流定律。對于正弦穩態交流電路分析,上式可寫為:
![]() (7-2-3)
(7-2-3)
對于圖7-2-1所示的網絡,設支路電流列向量為![]() ,該網絡的關聯矩陣已寫出,用A左乘i可得:
,該網絡的關聯矩陣已寫出,用A左乘i可得:
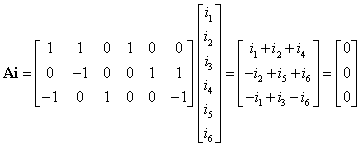
由式可見,![]() 的乘積列向量其實為n個節點的KCL方程式。
的乘積列向量其實為n個節點的KCL方程式。
在用節點電壓法解題時要用到節點電壓與支路電壓之間的關系。下面分析節點電壓與支路電壓之間關系的矩陣形式。設網絡各節點電壓的列向量為![]() ,(式中為使節點電壓與支路電壓相區別,在下標中用一加圈數字表示節點),參考節點的電壓為零。支路電壓列向量為
,(式中為使節點電壓與支路電壓相區別,在下標中用一加圈數字表示節點),參考節點的電壓為零。支路電壓列向量為![]() 。若用關聯矩陣的轉置矩陣
。若用關聯矩陣的轉置矩陣![]() 左乘節點電壓列向量
左乘節點電壓列向量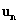 ,可得一個b 行的列矩陣。前已指出,A中每一列只包含二個元素(若支路連接于參考節點,則該列只包含一個元素),反映支路所連接的二個節點,且為一正一負,即支路方向離開節點為正,反之為負。因此與
,可得一個b 行的列矩陣。前已指出,A中每一列只包含二個元素(若支路連接于參考節點,則該列只包含一個元素),反映支路所連接的二個節點,且為一正一負,即支路方向離開節點為正,反之為負。因此與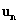 乘積的列向量第一行中只包含該支路離開節點的電壓與指向節點的電壓之差,即為該支路的支路電壓值。因此
乘積的列向量第一行中只包含該支路離開節點的電壓與指向節點的電壓之差,即為該支路的支路電壓值。因此![]() 左乘
左乘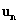 的值即為支路電壓列向量u,即有:
的值即為支路電壓列向量u,即有:
![]() (7-2-4)
(7-2-4)
對于正弦穩態交流電路有:
![]() (7-2-5)
(7-2-5)
對于圖7-2-1所示的網絡,其節點電壓列向量為![]() ,用
,用![]() 左乘
左乘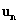 ,得
,得
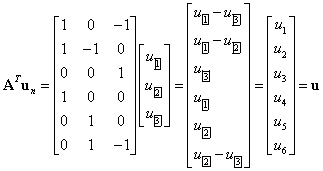
式(7-2-4)反映了節點電壓與支路電壓之間的關系。


 返回頂部
返回頂部 刷新頁面
刷新頁面 下到頁底
下到頁底