采樣定理在1928年由美國電信工程師H.奈奎斯特首先提出來的,因此稱為奈奎斯特采樣定理。
1933年由蘇聯(lián)工程師科捷利尼科夫首次用公式嚴格地表述這一定理,因此在蘇聯(lián)文獻中稱為科捷利尼科夫采樣定理。
1948年信息論的創(chuàng)始人C.E.香農(nóng)對這一定理加以明確地說明并正式作為定理引用,因此在許多文獻中又稱為香農(nóng)采樣定理。
奈奎斯特采樣定理解釋了采樣率和所測信號頻率之間的關(guān)系。 闡述了采樣率fs必須大于被測信號感興趣最高頻率分量的兩倍。
該頻率通常被稱為奈奎斯特頻率fN。即:
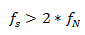
首先,我們要明確以下兩點:
- 采樣的目的是為了利用有限的采用率,無失真的還原出原有聲音信號的樣子。
- 奈奎斯特采樣定理也可以理解為一個正弦波每個周期最少取兩個點才能把正弦波還原回去。
為更好理解其原因,讓我們來看看不同速率測量的正弦波。
1. 假設(shè) fS = fN
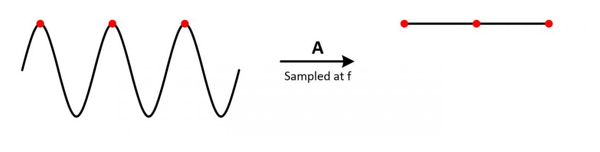
可以看出,無論我們從哪一點開始采樣,每次采集到的數(shù)據(jù)都是一樣的,對應(yīng)的頻率成分為0Hz。
2. 假設(shè) fS = (4/ 3) * fN
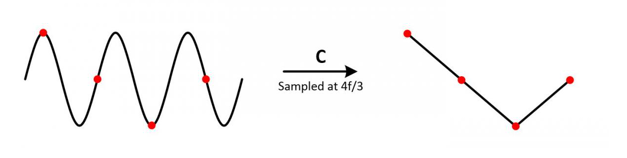
以上采樣到的曲線仍然無法還原原有波形的樣子。
3. 假設(shè) fS = 2 * fN
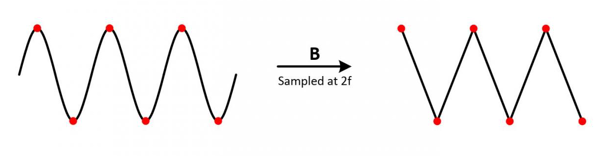
如上圖,將這些采樣點連成線條,得到的信號形狀為三角波,雖然信號的頻率成分沒有失信,但是很難保證信號的幅值不失真。因為這兩個采樣點很難位于正弦信號的波峰與波谷處。也就是說,在很大程度上,采樣后的信號的幅值是失真的。
我們再考慮如下情況:
假設(shè)一條正弦曲線為sin(2π/t),頻率為1Hz。我們以2Hz的頻率對該曲線進行采樣(每隔0.5s),可以得到3個紅色采樣數(shù)據(jù),如下圖:
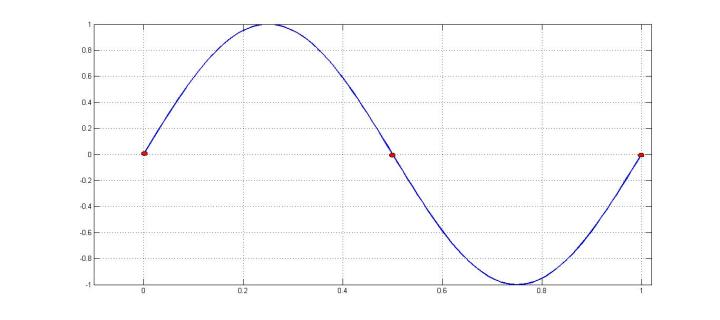
對于這三個點,我們不能確定它對應(yīng)的正弦曲線是sin(2π/t),因為sin(4π/t)等倍頻曲線也會穿過這三個紅色采樣點:
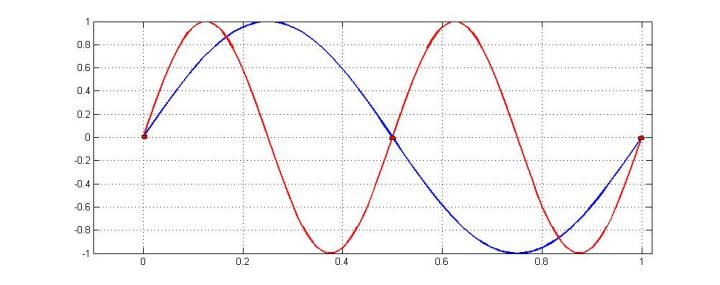
混疊
如果信號的采樣率低于兩倍奈奎斯特頻率,采樣數(shù)據(jù)中就會出現(xiàn)虛假的低頻成分。 這種現(xiàn)象便稱為混疊。
下圖顯示了800 kHz正弦波1MS/s時的采樣。虛線表示該采樣率時記錄的混疊信號。 800 kHz頻率與通帶混疊,錯誤地顯示為200 kHz正弦波。
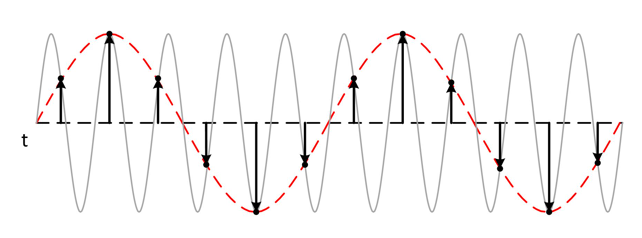
絕大多數(shù)信號都是能夠進行傅里葉變換的,就意味著,不管一個信號多么復(fù)雜,總可以分解為若干個正(余)弦信號的和,對應(yīng)了信號的頻率分量。因此,Nyquist采樣定理只需找到信號最大的頻率分量,再用2倍于最大頻率分量的采樣頻率對信號進行采樣,從理論上解決了,離散信號能夠重建出連續(xù)信號的問題。


 返回頂部
返回頂部 刷新頁面
刷新頁面 下到頁底
下到頁底