通信系統都有發送機和接收機,為了提高系統的可靠性,通常在接收機的輸入端接有一個帶通濾波器,信道內的噪聲構成了一個隨機過程,經過該帶通濾波器之后,則變成了窄帶隨機過程,因此,討論窄帶隨機過程的規律是重要的。
一、窄帶隨機過程的定義
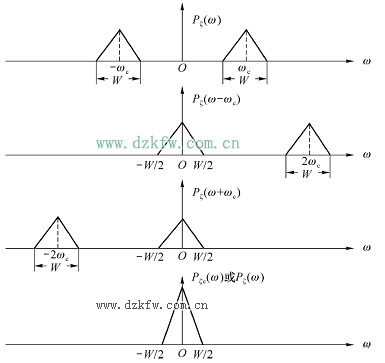
窄帶隨機過程的定義借助于它的功率譜密度的圖形來說明。圖3.5.1(a)中,波形的中心頻率為![]() ,帶寬為
,帶寬為![]() ,當滿足
,當滿足![]() 時,就可認為滿足窄帶條件。
時,就可認為滿足窄帶條件。
若隨機過程的功率譜滿足該條件則稱為窄帶隨機過程。
若帶通濾波器的傳輸函數滿足該條件則稱為窄帶濾波器。
隨機過程通過窄帶濾波器之后變成窄帶隨機過程。
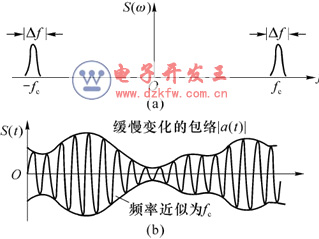
如果在示波器上觀察這個過程中一個樣本函數的波形,則會發現它像一個包絡和相位緩慢變化的正弦波,如圖3.5.1(b)所示。因此窄帶隨機過程可用下式表示成:
窄帶隨機過程也可用下式表示
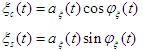
可見,
三、同相分量與正交分量的統計特性
設窄帶隨機過程是均值為零平穩的窄帶高斯過程。可以證明,它的同相分量和正交分量也是均值為零的平穩高斯過程,而且與
1.數學期望
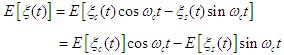
我們知道一些統計特性可以從自相關函數中得到,所以,按定義
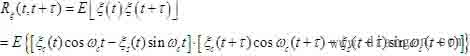
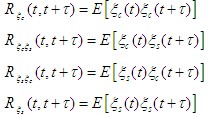
由于式(1)和式(2)相等,則應有
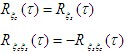
3.概率密度函數
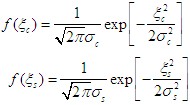
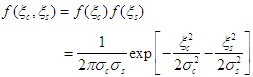
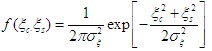
四、包絡與相位的統計特性
現在來確定窄帶平穩高斯過程的包絡和相位的統計特性,隨機包絡和隨機相位可表示為
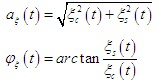
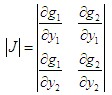
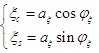
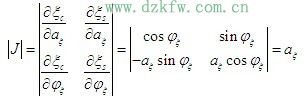
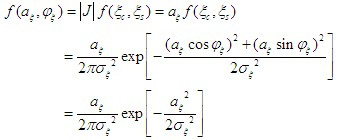
利用概率論中的邊際分布知識,可求得包絡
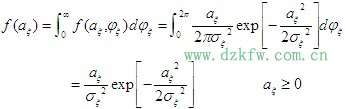
瑞利分布的特點:最大值發生在
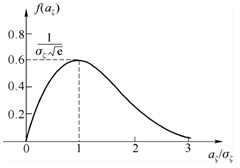
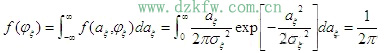
五、窄帶隨機過程的功率譜密度
結論:窄帶隨機過程同相分量

證明:窄帶隨機過程
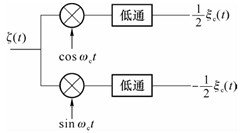
對式
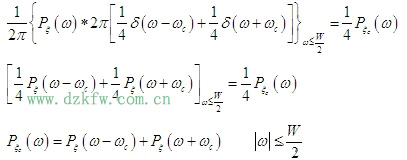
同理,對式
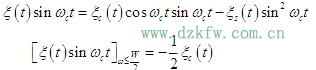



 返回頂部
返回頂部 刷新頁面
刷新頁面 下到頁底
下到頁底