一、磁感應強度矢量B
1、磁場的外在表現:
(1)對電流有作用力。
(2)對磁鐵有作用力。
(3)對運動電荷有作用力。
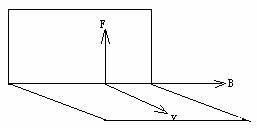
2、磁場對運動電荷作用力的特征
(1)有零力線方向:在磁場中總有一個特殊方向,當電荷在磁場中沿該方向運動時不受力,該方向稱為零力線方向,該方向與運動電荷無關,反映了磁場本身的性質,規定該方向為磁感應強度矢量B的方向。
(2)運動電荷受到的磁場作用力總是與零力線方向和速度方向垂直。
(3)當v與零力線方向有夾角α時,在任一點受力F∝qvsinα,當v與零力線方向垂直時受力最大,即F┴∝qv┴ 。
(4) 當q和v┴改變時,F┴的大小也改變,但比值F┴/(q v┴)在任一點總是常量,顯然,該比值反映了磁場在該點的性質,與運動試探電荷無關,我們可利用該比值來定義描述場本身特性的物理量 磁感應強度矢量B 。
3、磁感應強度矢量B的定義
在第一章中,問題的分析過程是:電荷間
有力的作用,引入電場,用試探電荷測量
電場,定義電場強度E,求出點電荷的場
強公式,引入場強疊加原理,根據點電荷的場強公式和場強疊加原理求場強分布(場強疊加法)。在本章中,也要引入場的概念,后給出產生場的規律。
磁場中某點的磁感應強度是一個矢量,其大小等于單位試探電荷以單位速率垂直零力線方向運動時在該點所受力的大小,其方向滿足v×B指向F的方向。其數學表示式為B=F/qV
 單位:特斯拉(T),1T=1×104G高斯
單位:特斯拉(T),1T=1×104G高斯
二、磁感應線(磁力線)
磁感應線:形象描述磁感應強度空間分布的曲線;實際上并不存在。
規定:
(1)磁感應線上任一點的切線方向等于該點磁感應強度矢量B的方向;
(2)垂直穿過單位面積的磁感應線的根數等于該點磁感應強度的大小。
三、畢奧—薩伐爾斯定律
畢奧 薩伐爾定律主要描述電流元產生的磁場的大小及方向的一個基本定律,它與電場中的點電荷的場強公式相對應,是一個實驗定律,但無法用實驗直接驗證。
在19 世紀20年代,畢奧和薩伐爾對電流產生的磁場分布作了許多實驗研究,并和拉普拉斯一起研究和分析了很多實驗資料,得到了對應微元段電流產生的磁感應強度計算公式。
1、電流元
設在真空中有電流強度為I的任意形狀的載流導線,其導線截面與所考察的場點P的距離比較可略去不計,這樣的電流稱為線電流。在線電流上取長為dl的定向線元dl,規定dl的方向與線元內的電流密度j的方向相同,并將乘積Idl稱為電流元。
2、畢奧 薩伐爾定律
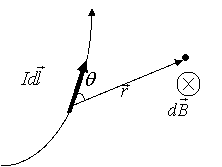
電流元Idl在任一場點P產生的磁場的磁感應強度dB的大小與電流元的大小Idl成正比,與電流元到P點的距離r的平方成反比,還與Idl同r之間夾角的正弦sinθ成正比。
分析表明,dB的方向總垂直于dl與r所構成的平面,并沿dl×r的方向(見圖),故可用矢量式表述為:
![]()
上式稱為畢奧—薩伐爾定律。
由畢奧—薩伐爾定律可知,電流元Idl產生的
dB所對應的磁感應線,是以Idl所在的延長線
為軸,以rsinθ為半徑的圓。在同一圓周上各點的dB相等,并隨r增大而減小,但位于軸線上各點的dB卻等于零。


 返回頂部
返回頂部 刷新頁面
刷新頁面 下到頁底
下到頁底