機(jī)械原理中,根據(jù)平面四連桿機(jī)構(gòu)中是否存在曲柄,有一個(gè)曲柄或兩個(gè)曲柄,可把它分為下面三種基本形式。
1,曲柄搖桿機(jī)構(gòu)
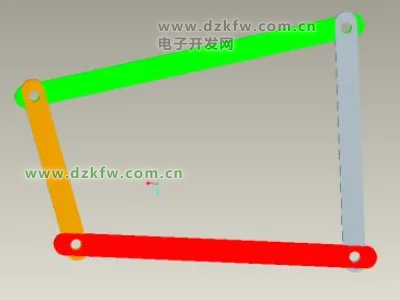
2,雙曲柄機(jī)構(gòu):平面四連桿機(jī)構(gòu)中若有兩個(gè)曲柄存在,這樣的機(jī)構(gòu)稱為雙曲柄機(jī)構(gòu)。這種機(jī)構(gòu)一般可將主動(dòng)件的勻速整周轉(zhuǎn)動(dòng)轉(zhuǎn)換成從動(dòng)件的非勻速或勻速整周轉(zhuǎn)動(dòng)。
雙曲柄機(jī)構(gòu)中,若兩曲柄的長度相等,且連桿與靜件的長度也相等,則此機(jī)構(gòu)為平行四邊形機(jī)構(gòu)。其運(yùn)動(dòng)特點(diǎn)是兩曲柄的角速度始終保持相等,連桿在運(yùn)動(dòng)過程中始終作平行移動(dòng)。若改變平行四邊形機(jī)構(gòu),使其兩個(gè)曲柄轉(zhuǎn)動(dòng)方向相反,這時(shí)的機(jī)構(gòu)稱為反向雙曲柄機(jī)構(gòu)。
3,雙搖桿機(jī)構(gòu):在平面四連桿機(jī)構(gòu)中,若與靜件相聯(lián)的兩桿件均為搖桿,則此機(jī)構(gòu)稱為雙搖桿機(jī)構(gòu)。
擴(kuò)展資料:
定理
1,桿長之和條件:平面四桿機(jī)構(gòu)的最短桿和最長桿的長度之和小于或者等于其余兩桿長度之和。
2,在鉸鏈四桿機(jī)構(gòu)中,如果某個(gè)轉(zhuǎn)動(dòng)副能夠成為周轉(zhuǎn)副,則它所連接的兩個(gè)構(gòu)件中,必有一個(gè)為最短桿,并且四個(gè)構(gòu)件的長度關(guān)系滿足桿長之和條件。
3,在有整裝副存在的鉸鏈四桿機(jī)構(gòu)中,最短桿兩端的轉(zhuǎn)動(dòng)副均為周轉(zhuǎn)副。此時(shí),如果取最短桿為機(jī)架,則得到雙曲柄機(jī)構(gòu);若取最短桿的任何一個(gè)相連桿為機(jī)架,則得到曲柄搖桿機(jī)構(gòu);如果取最短桿對(duì)面構(gòu)件為機(jī)架,則得到雙搖桿機(jī)構(gòu)。
4,如果四桿機(jī)構(gòu)不滿足桿長條件,則不論選取哪個(gè)構(gòu)件為機(jī)架,所得到機(jī)構(gòu)均為雙搖桿機(jī)構(gòu)。
上述系列結(jié)論稱為格拉霍夫定理。


 返回頂部
返回頂部 刷新頁面
刷新頁面 下到頁底
下到頁底