導(dǎo)讀：分別介紹雷諾數(shù)和馬赫數(shù)的物理意義，分析他們對流動的具體影響。

雷諾數(shù)
我們已經(jīng)知道，雷諾數(shù)的表達式是這樣的： 表達式中的  是流體的粘性系數(shù)，所以雷諾數(shù)與粘性有關(guān)。粘性是流體運動時內(nèi)部產(chǎn)生剪切力的象征，所以雷諾數(shù)就表示了粘性力的大小了。還有慣性力，書上說，雷諾數(shù)表示了慣性力與粘性力之比。慣性力是速度的變化強度，所以雷諾數(shù)就表示了粘性力對流動的影響程度。粘性從而產(chǎn)生剪切力，還有一個額外的影響是流態(tài)。低雷諾數(shù)時流動傾向于層流，高雷諾數(shù)時流動傾向于塔留，這是粘性作為阻尼作用對流動的影響。

 

 

歷史上，雷諾數(shù)的提出經(jīng)過了幾個階段，最先提出這個概念的人是斯托克斯，就是NS方程中的S；當(dāng)然雷諾數(shù)名字來源于雷諾，是他首先提出雷諾數(shù)數(shù)的表達式；但是真正把這個無量綱數(shù)稱為雷諾數(shù)的人，是研究了流體穩(wěn)定性的索末菲。我們來看一下雷諾數(shù)為什么表示了慣性力與粘性力之比，把雷諾數(shù)的分子和分母分別乘以速度和尺度，整理后，得到這樣的表達式： 分子中密度與尺度三次方相乘表示了質(zhì)量，速度平方與尺度的比值表示了加速度。分子中的兩項則分別表示了剪切應(yīng)力和面積，這樣就可以看出分子表示了慣性力的大小，分母表示了粘性力的大小。
 

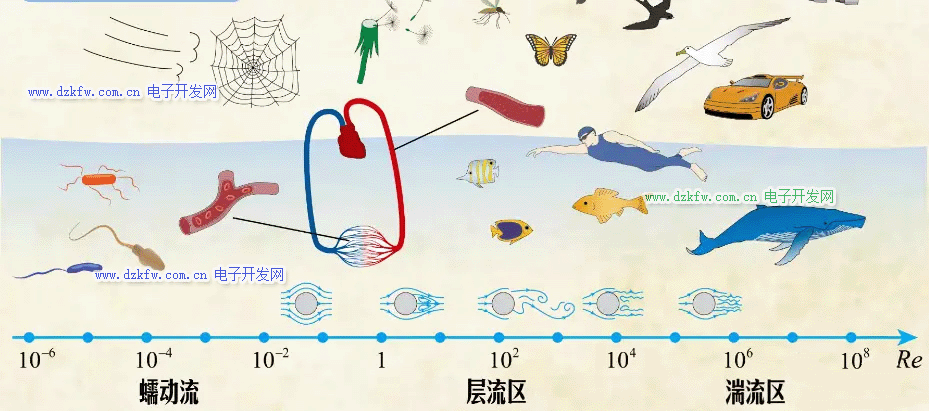
下面我們在描述運動的NS次方程中看看雷諾數(shù)的影響。這是簡化的x方向動量方程： 現(xiàn)在因為一些流場的特征量來對其進行無量綱化： 假設(shè)直到  為流場特征量，帶星的變量就是無量綱的了。將這些關(guān)系式代入到上面的方程中，整理后就得到了無量綱的方程： 無量綱方程可以用來描述任何幾何相似，邊界條件相同的流動。可以看到，相比有量綱方程，無量綱方程中多了兩項，這兩項分別對應(yīng)兩個無量綱數(shù)，一個是歐拉數(shù)  ，一個是雷諾數(shù)的倒數(shù)  。歐拉數(shù)表示了壓力與慣性力之比，當(dāng)使用壓差力分析問題時并不起作用，所以影響整個方程的就只剩下雷諾數(shù)了。雷諾數(shù)影響無量綱方程預(yù)示著幾何相似的流動，如果雷諾數(shù)不同，流動就不同。雷諾數(shù)出現(xiàn)在粘性項的分母中，它越大，粘性項的影響就越小。當(dāng)雷諾數(shù)遠遠大于1時，粘性力趨向于零。這時，運動只由壓差力決定： 可以想象這對應(yīng)于流動符合伯努利方程的情況。當(dāng)雷諾數(shù)遠遠小于1時，粘性力非常大，任何壓差產(chǎn)生的驅(qū)動力都會被幾乎同等大小的粘性力抵消，所以流體很難產(chǎn)生加速度。可以說毫無慣性可言，慣性力是可以忽略。這時粘性力與壓差力平衡： 這種流動非常符合亞里士多德的描述，就是力是維持物體運動的原因，一旦驅(qū)動力消失，巨大的粘性力就會立刻讓運動停下來，一步也不多走。這里給出了一些常見運動的雷諾數(shù)：

 

 

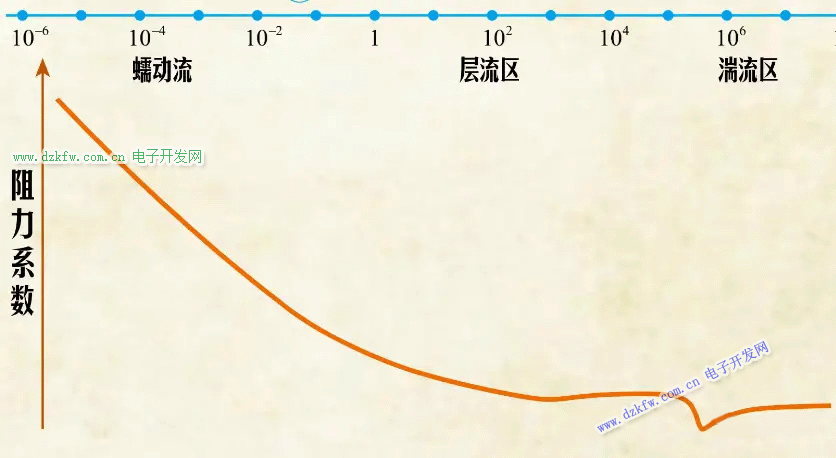
下面是液體中，上面是氣體中。雷諾數(shù)遠小于1的流動又稱為蠕動流，也稱為斯托克斯流動；還有一些運動的雷諾數(shù)不高，粘性力也不算大，流動為層流；而常見的多數(shù)流動雷諾數(shù)比較大，處于湍流區(qū)。以繞圓球流動為例，這是其阻力系數(shù)隨雷諾數(shù)的變化規(guī)律。在低雷諾數(shù)范圍內(nèi)，隨著雷諾數(shù)的增大，粘性作用減弱，阻力迅速變小。當(dāng)雷諾數(shù)達到一定范圍后阻力不再隨雷諾數(shù)變化。

 

 

再增加雷諾數(shù)，阻力還會有突然減小然后又突然增大的現(xiàn)象。規(guī)律這么復(fù)雜的原因是阻力并不僅僅由粘性力構(gòu)成。在蠕動流狀態(tài)下，流體繞球流動，看起來前后是對稱的，其實并不完全是。前后的流速是對稱的，但壓力并不對稱。這時流動阻力主要是由流體與球表面之間的摩擦力造成的。在中等雷諾數(shù)下流動為層流，但非定常性可能很強。這時，流體繞過球后形成規(guī)則的脫落渦，即卡門渦街：

 

 

球除了受到阻力之外，還受到周期性的橫向激振力。湍流是更常見的流動，比如這個網(wǎng)球后的流動。網(wǎng)球后的流動很亂，找不到規(guī)律，這時球的阻力主要由前后的壓差力產(chǎn)生，摩擦力只占一小部分。定量來看，蠕動流中粘性力產(chǎn)生的摩擦阻力占總阻力的三分之二，而一般的高雷諾數(shù)下摩擦阻力只占總阻力的10%或更少。湍流中的雷諾數(shù)：我們知道，湍流都是對應(yīng)很高的雷諾數(shù)。也就是粘性力很小的時候，由于其內(nèi)部存在著復(fù)雜的剪切流動結(jié)構(gòu)，湍流對雷諾數(shù)的變化是很敏感的。比如在這個火山噴發(fā)的湍流流動中，含有復(fù)雜的大大小小的渦團。圓圈所示的大概是這個流動中最大的渦團尺寸。

 

 

放大仔細(xì)看，這樣的小渦流大概是流動中最小的。

 

 

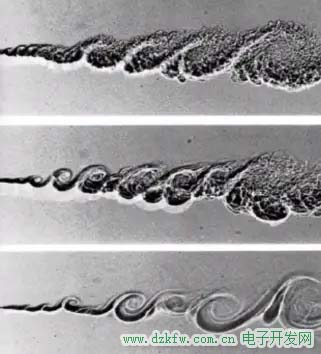
渦團這個小渦的尺寸實際上是受雷諾數(shù)影響的，因為粘性耗散會讓過小的渦迅速停下來，宏觀動能轉(zhuǎn)化為內(nèi)能。雷諾數(shù)越大，粘性作用越小，渦可以維持的尺寸就越小。流場中的大渦尺寸是由邊界條件決定的，比如這個流動中的大渦尺寸是由火山口的尺寸決定的。對于下面這種剪切流動，從下至上雷諾數(shù)越來越大。

 

 

大渦的尺寸不變，而小渦的尺寸越來越小，最下面的流動其實是層流流動，因為只有大渦而沒有小渦，最上面的流動含有豐富的小渦，是典型的湍流。對于湍流可以總結(jié)出這樣一個關(guān)系式：   表示大渦尺寸，  表示小渦尺寸，可見增大雷諾數(shù)可以拉開大小渦的差距。這也可以用來理解為什么低雷諾數(shù)對應(yīng)著層流，因為低雷諾數(shù)下小渦尺寸和大渦差距不大，形不成能級傳遞過程。雷諾數(shù)表達式中的速度和尺度是一個容易讓人困惑的問題。書上說，應(yīng)該用特征，速度和特征尺度。 可是，啥是特征呢？這個問題還真不簡單，要具體問題具體分析。不過我們可以看看選取原則。對于平板邊界層流動，一般經(jīng)常選用的是流向長度。而實際上更合理的尺度是當(dāng)?shù)氐倪吔鐚雍穸龋�因為它與當(dāng)?shù)卣承粤χ苯酉嚓P(guān)。想起流向長度完全是為了方便并不是很合理。不過，考慮到邊界層厚度和流向長度有一定關(guān)系，選取流向長度也是可以接受的。

 

 

對于管流，距進口足夠遠處的流動與進口無關(guān)，就不能選取流向長度了。這時最方便也比較合理的尺度，是管道直徑。對于繞機翼和繞圓柱流動，通常選取弦長和圓柱直徑，也是考慮方便性，其實這兩種流動中更合理的尺度也是邊界層厚度。

 

 

馬赫數(shù)
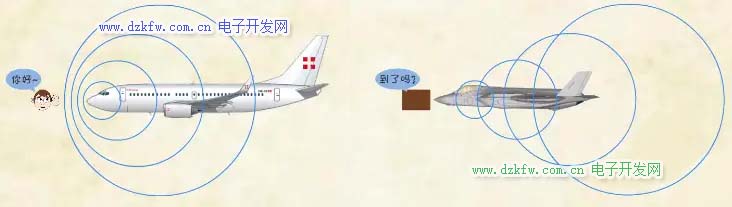
現(xiàn)在我們來看看影響流動的另一個重要的無量綱數(shù)-馬赫數(shù)。馬赫數(shù)是運動速度與當(dāng)?shù)匾羲僦�比，是馬赫提出來的： 對于理想氣體因素，只與氣體種類和溫度有關(guān)： 音速是聲音的傳播速度，也就是氣體中小的壓力擾動的傳播速度。這個傳播速度大概與氣體分子的平均熱運動速度相當(dāng)。當(dāng)飛機在空氣中運動時，它時刻都對空氣產(chǎn)生小擾動，擾動以音速傳播。如果飛機的運動速度沒有聲音快，聲音就會比飛機更早到達前方。如果有人處在亞音速飛機的前方，通過聲音就可以知道飛機來了。如果飛機的運動速度比聲音還快，它就會比聲音更早到達前方。如果有人處在超音速飛機的前方，他是無法通過聲音直到飛機來了的。

 

 

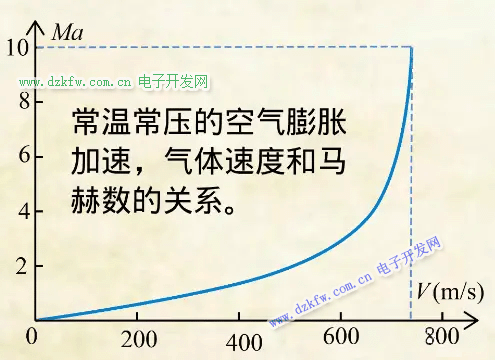
物體運動時會推擠ta前面的空氣,產(chǎn)生的壓力波會'通知'前方的氣體讓路。若物體運動速度太快，前方氣體來不及跑就會被壓縮。如果讓大氣靠自身的膨脹加速流動，則其速度與對馬赫數(shù)的關(guān)系是這樣的：

 

 

可以看出，當(dāng)馬赫數(shù)達到10時，速度只有每秒七百多米。事實上這樣加速下去，理論上馬赫數(shù)無窮大時流速也不到每秒八百米。超高的馬赫數(shù)其實是膨脹降溫引起的音速降低產(chǎn)生的可見，馬赫數(shù)并不對應(yīng)速度的大小，因為音速并不是常數(shù)。為了理解馬赫數(shù)的物理意義，我們先來看另一個無量綱數(shù)科西數(shù)。這是柯西數(shù)的表達式： 它的定義是氣體中的慣性力與彈性力之比，其中的體積彈性模量E與體積變化和產(chǎn)生的壓力有關(guān)： 通過一些關(guān)系式的變化，可以導(dǎo)出科西數(shù)等于馬赫數(shù)的平方： 所以我們也可以說，馬赫數(shù)表示了慣性力與彈性力之比。在流動中，馬赫數(shù)的大小體現(xiàn)了氣體在慣性力作用下受壓縮的程度。這里給出了一些常見運動的馬赫數(shù)范圍，可以根據(jù)馬赫數(shù)范圍，把流動分為不可壓縮流動，亞音速，超音速和高超音速。

 

 

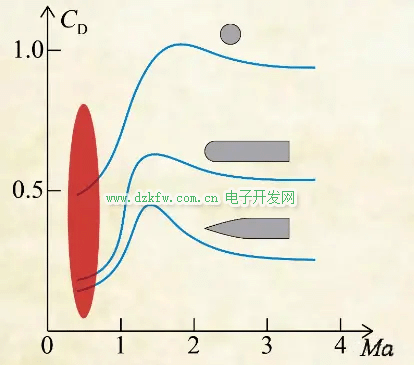
基本上所有生物的活動都屬于不可壓流動，這時馬赫數(shù)不影響流動。亞音速流動中馬赫數(shù)對流動的影響主要是壓縮性方面；跨音速流動的主要特點是出現(xiàn)了激波；超音速流動受激波影響，并且出現(xiàn)了壓縮和摩擦引起的氣動加熱問題；高超音速流動則由于氣動加熱溫度過高，還產(chǎn)生了氣體電離等問題。這是幾種形狀的物體的阻力系數(shù)，隨馬赫數(shù)的變化： 

 

 

在亞音速范圍內(nèi)，完全沒有激波時，阻力系數(shù)就已經(jīng)隨馬赫數(shù)而增大了，這完全是由壓縮性帶來的，可以用壓力系數(shù)定義是來解釋，這是可壓縮流動中的總靜壓關(guān)系：  除了慣性力產(chǎn)生的動壓之外，額外的項是彈性力帶來的，也就是說，減速時彈性力會帶來額外的壓力。根據(jù)壓力系數(shù)的定義： 如果流動是不可壓縮的，滯止點的  等于1，如果流動是可壓縮的，滯止點的  大于1。也就是說，壓縮性使同樣的減速產(chǎn)生更大的壓力，從而帶來更大的阻力。至于跨音速和超音速時阻力系數(shù)大，原因則是激波阻力產(chǎn)生的。

雷諾數(shù)與馬赫數(shù)對流動的影響
 真實流動中。雷諾數(shù)和馬赫數(shù)是同時起作用的，我們分幾種情況分析一下，首先來看一個有點奇怪的問題——伯努利方程適用的雷諾數(shù)和馬赫數(shù)范圍是什么？伯努利寫的流體力學(xué)書里面曾經(jīng)用這樣的例子說明伯努利原理：

 

 

但如果實際做這個實驗，就會發(fā)現(xiàn)這個流動完全不符合伯努利原理。原因是在管流中粘性力起決定性作用，而沿流向應(yīng)用伯努利方程的條件是定常、不可壓、無粘。很顯然，湍流屬于非定常流動，所以定常的條件限制了流動必須是不可壓。不可壓是不可能絕對滿足的，不過馬赫數(shù)足夠小時，流動幾乎是不可壓的。無粘也不可能絕對滿足，粘性很小的流動對應(yīng)的是雷諾數(shù)足夠大。然而問題是，當(dāng)雷諾數(shù)足夠大時，流動就會使湍流，所以雷諾數(shù)足夠大，并不能保證流動滿足伯努利方程。
現(xiàn)在來分析下面管道流動：

 

 

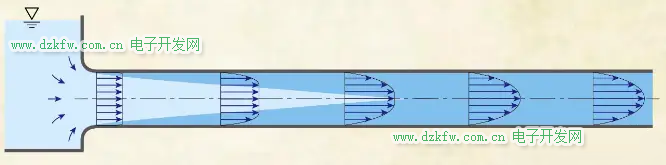
它并不是典型的管道流動，而是和管道的入口段流動類似，壁面的邊界層很薄，主流是滿足伯努利方程的。邊界層的影響是改變了主流的有效流通面積，所以伯努利方程還是可以計算這類問題的，但面積要做修正。
然而，要滿足這種流動是有條件，就是雷諾數(shù)要足夠高。如果雷諾數(shù)很低，邊界層就很厚，就會像圖中所示這樣占滿通道，伯努利方程就完全不適用了。

 

 

伯努利原理大概是最深入人心的流體力學(xué)知識了，其實它的適用范圍很有限，之所以貌似應(yīng)用廣泛，是因為人類的活動大約符合他。如果是細(xì)菌來寫流體力學(xué)書，伯努利原理就完全不會出現(xiàn)，反而是亞里士多德的“力是維持物體運動的原因”會被奉為經(jīng)典。而對超音速飛機而言，激波和膨脹波才是流動的主旋律。即使在我們身邊，也并不存在精確滿足伯努利方程的流動，使用它時要小心。
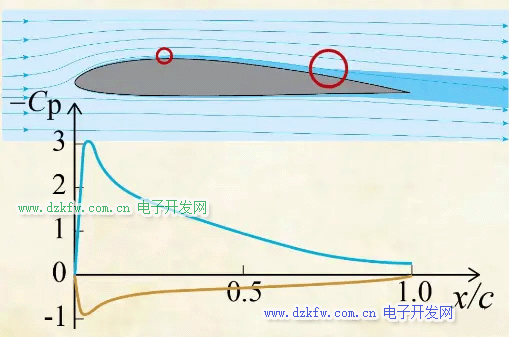
當(dāng)流動馬赫數(shù)很低時，雷諾數(shù)是流動的主要決定因素，比如這個繞機翼的低速流動中，外流是符合伯努利方程的。雷諾數(shù)通過影響邊界層厚度而影響外流的壓力分布。這其中還有兩個更大的影響，就是雷諾數(shù)會影響邊界層轉(zhuǎn)捩點和分離點。

 

 

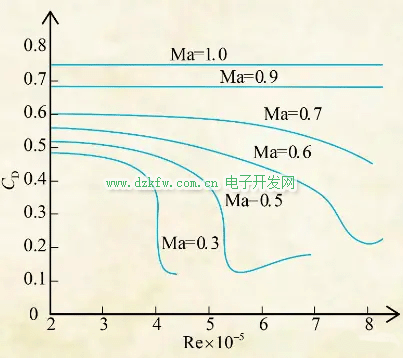
轉(zhuǎn)捩使邊界層增厚，對外流有一定向外排擠的作用。分離使邊界層離開，避免對外流有非常大的向外排擠作用。邊界層厚度通常很薄，本身的一點變化對主流影響很小。而轉(zhuǎn)變和分離就不同了，經(jīng)常是繞物體流動問題中最大的影響因素。如果流動是無粘且不可壓的，壓力分布本來與流速是無關(guān)的，或者說流動是受雷諾數(shù)和馬赫數(shù)的影響，而不是流速和尺度本身。對于高速流動，馬赫數(shù)通常是流動的決定性因素，這個圖表示了球的阻力系數(shù)：

 

 

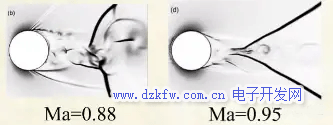
隨雷諾數(shù)和馬赫數(shù)的變化可以看出，低馬赫數(shù)下阻力系數(shù)隨雷諾數(shù)變化很大；而當(dāng)馬赫數(shù)接近1時，阻力系數(shù)基本不再隨雷諾數(shù)變化了。這是因為這時激波是流動的主要決定因素。

 

 

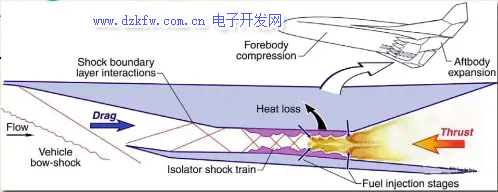
對于跨音速和超音速的流動，經(jīng)常不考慮雷諾數(shù)的影響，原因有兩點，一是激波的影響遠大于粘性；二是高馬赫數(shù)通常對應(yīng)著高雷諾數(shù)。而雷諾數(shù)足夠高以后，流動就不怎么受雷諾數(shù)受影響了，但也有例外，比如這個高超音速沖壓發(fā)動機中，雷諾數(shù)和馬赫數(shù)就都是重要的。