第五講 邏輯函數的卡諾圖化簡法
2.5 邏輯函數的卡諾圖化簡法
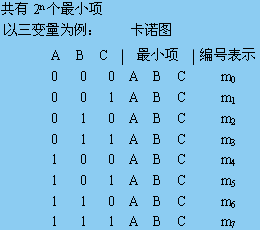
2. 5. 1 最小項與卡諾圖
一、最小項的定義和性質
1.最小項的定義
2.最小項的基本性質
二、表示最小項的卡諾圖
1.相鄰最小項
2.最小項的卡諾圖表示
2. 5. 2 用卡諾圖表示邏輯函數
一、邏輯函數的標準與-或式
二、用卡諾圖表示邏輯函數
1.已知邏輯函數式為標準與-或式,畫邏輯函數卡諾圖。
2.已知邏輯函數真值表,畫邏輯函數卡諾圖
3.邏輯函數為一般表達式時,畫邏輯函數卡諾圖。
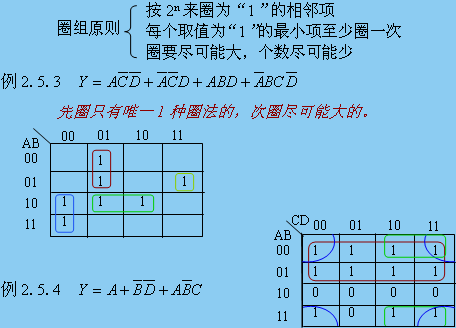
2. 5. 3 用卡諾圖化簡邏輯函數
2. 5. 4 具有無關項的邏輯函數的化簡
一、邏輯函數中的無關項
二、利用無關項化簡邏輯函數
作業:P36 2.6(1)(3)(5)(7)(9) 2.10(2)(4)
2.5 邏輯函數的卡諾圖化簡法
2. 5. 1 最小項與卡諾圖
一、最小項的定義和性質
1.最小項的定義
特點:每項都有n個變量
每個乘積它中每個變量出現且僅出項1次
2.最小項的基本性質
a.只有一組取值使之為“1”
b.任二最小項乘積與“0”
c.所的最小項之和為“1”
二、表示最小項的卡諾圖
1.相鄰最小項
邏輯相鄰項——只有一個變量取值不同其余變量均相同的最小項
兩個相鄰最小項可以相加合并為一項,同時消去互反變量,合并結果為相同變量。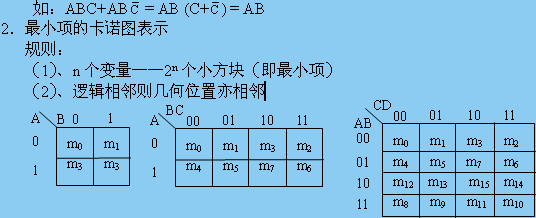
對于五變量及以上的卡諾圖,由于很復雜,在邏輯函數的化簡中很少使用。
2. 5. 2 用卡諾圖表示邏輯函數
一、邏輯函數的標準與-或式
如一個或邏輯式中的每一個與項都是最小項,則該邏輯式叫做標準與-或式,又稱為最小項表達式,并且標準與-或式是唯一的。
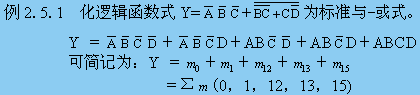
二、用卡諾圖表示邏輯函數
1.最小項表達式 卡諾圖
例2. 5. 2 試畫出例2. 5. 1中的標準與-或式的卡諾圖。
解:(1)畫出4變量最小項卡諾圖,如圖2. 5. 4所示。
2.真值表 卡諾圖
邏輯函數真值表和邏輯函數的標準與-或式是—一對應的關系,所以可以直接根據真值表填卡諾圖。
3.一般表達式樣 卡諾圖
(1)、化為最小項表達式
(2)、把卡諾圖中含有某個與項各變量的方格均填入1,直到填完邏輯式的全部與項。
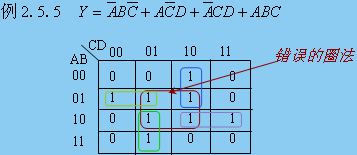
2.5.3 用卡諾圖化簡邏輯函數
步驟:①畫卡諾圖 ②正確圈組 ③寫最簡與或表達式
2. 5. 4 具有無關項的邏輯函數的化簡
一、邏輯函數中的無關項

用“×”(或“d” )表示
利用無關項化簡原則:
①、 無關項即可看作“1”也可看作“0”。
②、 卡諾圖中,圈組內的“×”視為“1”,圈組外的視為“0”。
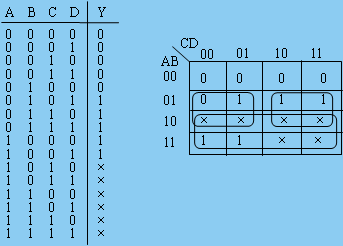
例2. 5. 6 為8421BCD碼,當其代表的十進制數≥5時,輸出為“1”,求Y的最簡表達式。(用于間斷輸入是否大于5)
解:先列真值表,再畫卡諾圖
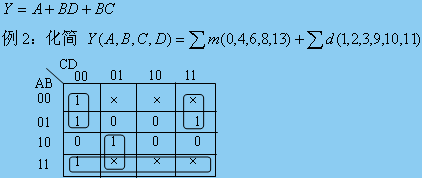


 返回頂部
返回頂部 刷新頁面
刷新頁面 下到頁底
下到頁底