一、歐姆定律  電阻

穩恒電場和靜電場一樣，滿足環路定律∮E·dl=0 ，從而可以引進電位差（電壓）的概念。加在導體兩端電壓不同，通過該導體的電流強度也不同。

歐姆定律：實驗證明，通過一段導體的電流強度與導體兩端的電壓成正比 ，即：

U=IR

式中的比例系數由導體的性質決定，叫做該導體的電阻，單位：歐姆（Ω）。

以電壓U為橫坐標，電流強度I為縱坐標畫出的曲線叫做該元件伏安特性曲線。

適用范圍：1、線性元件。2、不含源

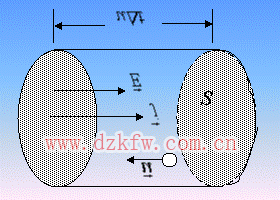
二、電阻率

實驗表明，導體的電阻與導體的材料、幾何形狀及溫度有關，對一定材料制成的橫截面均勻的導體，它的電阻為：

ρ由導體的材料決定，稱為導體的電阻率，描寫導體本身的性質。實驗證明，對于一般導體其隨溫度的變化可近似表示為：

式中ρ和ρ₀分別是攝氏溫度為t和0時的電阻率，α稱為溫度系數，取決于材料的種類。

電阻的計算：

當導體的截面S或電阻率ρ不均勻時，則其電阻計算式為：

式中dl為沿電流方向的長度元，計算時要注意電流是沿什麼方向流過導體的，S為垂直于電流方向的面積。

     超導現象簡介。

三、歐姆定律微分形式

經典金屬電子論：金屬導電的宏觀規律是由它的微觀結構和導電機制所決定的。下面我們從經典力學和經典統計學的角度對金屬導電的二個規律作一個粗糙的解釋。導體內無電場時，大量自由電子無規則熱運動的統計結果是不形成宏觀電流是；導體中加了電場以后，自由電子的總速度是由熱運動速度和定向運動速度兩部分速度組成。

自由電子平均定向運動速度（漂移速度）,不是對某一單個電子而言的，而是對大量電子求統計平均得到的物理量。例如，自由電子在穩恒電場作用下運動，與晶體點陣碰撞后，定向運動速度。電子在兩次碰撞之間的定向運動部分就是一個初速為零的勻加速直線運動（）。

下面分三步找關系：

1、        

設兩次碰撞之間的平均路程（平均自由程）為，由于熱運動平均速度遠大于定向平均速度，故近似有：

     

2、設穩恒電流I沿軸線方向均勻流過圓柱形均勻導體,所有自由電子以同一平均定向速度u運動,單位體積中自由電子數為n，則該柱體內共有nusΔt個自由電子，在時間Δt內全部通過橫截面s。

 ∴    

3、由上面得到：

令

則：

此式反映了電流密度j與引起這一電流密度的外因（E）及內因（σ）之間的關系，與歐姆定律I=GU（歐姆定律的積分形式）類似，稱為歐姆定律的微分形式，兩種形式是等價的，彼此可以互推。

簡單說明：    

它的物理意義是：電荷的定向運動是電場作用的結果，導體中某點的電流密度j與該點的電場強度E成正比。這一規律雖然是用經典理論在特殊情況下推導出來的，但是理論和實驗都證明，它對非穩恒情況的導體也成立。

四、焦爾定律——能量守恒定律的體現

英國物理學家焦耳通過實驗總結出如下規律：電流通過導體時放出的熱量Q與電流強度I的平方，導體的電阻R及通電的時間t成正比，當各個物理量均采用國際單位制時，Q=I²Rt，Q的單位為焦耳。

電流通過導體時放出焦耳熱的現象可從微觀上作定性分析與闡釋。自由電子與原子實通過碰撞交換能量，有電場時，把定向運動的動能傳遞給原子實，加劇了原子實的熱振動，這在宏觀上表現為導體的溫度升高，亦即金屬導體放出熱量。由此可見，焦耳熱實際上是電場力的功轉化而成的。

可以證明電場力的功正好等于導體在相同時間內所放出的焦耳熱.

設導體中的電流強度為I，則時間t內通過導體任一橫截面的電荷量為q=It，或者說有這麼多電量從導體的一端移至另一端，故電功為A=qU=IUt,對純電阻電路U=IR,∴A=I²Rt，A=Q這正是能量守恒定律所要求的結果。

假若電路是由導線和直流電動機組成的，電場力所做的功一小部分轉化為熱能，由導線釋放，大部分轉化為機械能，由電動機對外做機械功。此時從能量守恒定律就不能得出A=Q，但Q=I²Rt(實驗總結)與A=IUt(理論計算結果)仍然成立。對于純電阻電路，兩者等價；對于非純電阻電路，兩者不等價（不能得出A=Q ）。

電功率：單位時間內電場力所做的功稱為電功率，用P表示。

注意：P=UI與P=I²R或，是有區別的。UI是一段電路所消耗的全部電功率，而I²R或只是由于電阻發熱而消耗的電功率。當電路中只有電阻元件時，消耗的電能全部轉化成熱，這兩種功率是一樣的。但是，當電路中除了電阻外還有電動機、電解槽等其它轉化能量的裝置時，這兩種功率并不相等，必須分別計算。