帶電粒子在勻強(qiáng)磁場中的運(yùn)動是高考物理常見考題，在這篇文章中，我們把一些關(guān)鍵的物理量及解題思路做一個梳理。

關(guān)鍵物理量梳理

洛倫茲力

當(dāng)電荷速度方向與磁場方向垂直時，洛倫茲力的大小f=Bvq；當(dāng)電荷運(yùn)動方向與磁場方向夾角為θ時，洛倫茲力的大小f=Bvqsinθ；不難看出，洛倫茲力最大的特點(diǎn)就是大小與速度有關(guān)。

磁場對靜止的電荷無作用力，磁場只對運(yùn)動電荷有作用力，這與電場對其中的靜止電荷或運(yùn)動電荷總有電場力的作用是不同的。

洛倫茲力的方向始終與運(yùn)動的速度方向垂直，可通過左手定則來判定。

帶電粒子在洛倫茲力的作用下（充當(dāng)向心力），可以做勻速率圓周運(yùn)動。

荷質(zhì)比

帶電粒子的電荷量和其質(zhì)量的比值叫荷質(zhì)比，即k=q/m。對某種固定的粒子，其荷質(zhì)比是常量。例如，電子的比荷為e/me=1.758×10^11C/kg。

偏轉(zhuǎn)半徑

帶電粒子在勻強(qiáng)磁場中的運(yùn)動，在只有洛倫茲力作用下，粒子做圓周偏轉(zhuǎn)，其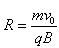半徑公式為：

由此可見，粒子的半徑僅與荷質(zhì)比、速度、磁場大小相關(guān)。

偏轉(zhuǎn)角

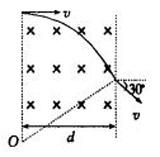
粒子在偏轉(zhuǎn)中，與原始速度矢量間夾角稱之為偏轉(zhuǎn)角。如下圖所示，經(jīng)歷了一段圓弧的偏轉(zhuǎn)后，粒子的偏轉(zhuǎn)角為30°；

需要注意的是，粒子偏轉(zhuǎn)角等于其偏轉(zhuǎn)弧所對應(yīng)的圓心角。這是初中幾何中講過的弦切角定理。

周期

帶電粒子在勻強(qiáng)磁場中的運(yùn)動，在只有洛倫茲力作用下，粒子做圓周偏轉(zhuǎn)，其周期公式為：

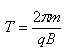
解題思路梳理

帶電粒子在勻強(qiáng)磁場中的運(yùn)動類問題通用解題步驟

（1）明確軌跡。

帶電粒子運(yùn)動為圓周運(yùn)動，需要同學(xué)們首先確定好運(yùn)動軌跡。有些題是沒有明確告訴你軌跡的，需要你自己分析，自己去畫圖（草圖），有時候畫出來圖還要接著修改。

（2）找圓心。

確定了大致的運(yùn)動軌跡，就開始研究圓心。圓心一般是兩個點(diǎn)的速度的垂線交點(diǎn)。

（3）構(gòu)建合適的三角形。

結(jié)合題意條件，構(gòu)建一個直角三角形，并在其中表述偏轉(zhuǎn)半徑R；一般要用到很多幾何知識。

（4）結(jié)合偏轉(zhuǎn)半徑的物理公式進(jìn)行求解。

有了半徑R之后，結(jié)合上述物理公式R=mv/Bq；就可以求解出來你需要的物理量了。

解題中三個物理量的確定

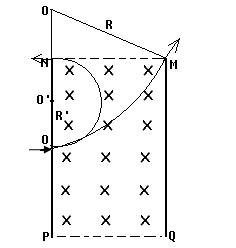
⒈圓心的確定

圓心一定在與速度方向垂直的直線上，根據(jù)入射點(diǎn)和出射點(diǎn)的速度方向做出垂線，交點(diǎn)即為圓心。

⒉半徑的計(jì)算

一般是利用幾何知識解直角三角形。

⒊帶電粒子在有界磁場中運(yùn)動時間的確定

利用圓心角和弦切角的關(guān)系或四邊形內(nèi)角和等于360度或速度的偏向角（帶電粒子射出磁場的速度方向與射入磁場的速度方向之間的夾角）等于圓弧軌道所對的圓心角，再由公式t/T=θ/360來求運(yùn)動時間。

找圓心、畫軌跡是解題的基礎(chǔ)

帶電粒子垂直于磁場進(jìn)入一勻強(qiáng)磁場后在洛倫茲力作用下必作勻速圓周運(yùn)動，抓住運(yùn)動中的任兩點(diǎn)處的速度，分別作出各速度的垂線，則二垂線的交點(diǎn)必為圓心；或者用垂徑定理及一處速度的垂線也可找出圓心；再利用數(shù)學(xué)知識求出圓周運(yùn)動的半徑及粒子經(jīng)過的圓心角從而解答物理問題。

導(dǎo)致軌道半徑變化的原因歸納

①帶電粒子速度變化導(dǎo)致半徑變化。如帶電粒子穿過極板速度變化；帶電粒子使空氣電離導(dǎo)致速度變化；回旋加速器加速帶電粒子等。

②磁場變化導(dǎo)致半徑變化。如通電導(dǎo)線周圍磁場，不同區(qū)域的勻強(qiáng)磁場不同；磁場隨時間變化。

③動量變化導(dǎo)致半徑變化。如粒子裂變，或者與別的粒子碰撞；

④電量變化導(dǎo)致半徑變化。如吸收電荷等。總之，由看m、v、q、B中某個量或某兩個量的乘積或比值的變化就會導(dǎo)致帶電粒子的軌道半徑變化。

臨界問題解題思路

帶電粒子在磁場中運(yùn)動的臨界問題的原因有：粒子運(yùn)動范圍的空間臨界問題；磁場所占據(jù)范圍的空間臨界問題，運(yùn)動電荷相遇的時空臨界問題等。審題時應(yīng)注意恰好，最大、最多、至少等關(guān)鍵字。

尋找產(chǎn)生極值的條件的常用思路梳理：

①直徑是圓的最大弦；

②同一圓中大弦對應(yīng)大的圓心角；

③由軌跡確定半徑的極值。