會員中心
會員注冊| 一、畢奧-薩伐爾定律 |
1.畢奧-薩伐爾定律:載流導線產(chǎn)生磁場的基本規(guī)律。微分形式為： 整個閉合回路產(chǎn)生的磁場是各電流元所產(chǎn)生的元磁場dB的疊加。 |
 |
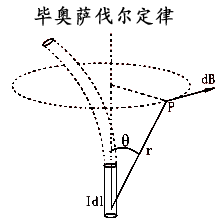| 磁感應線的方向服從右手定則，如圖。 |
 |
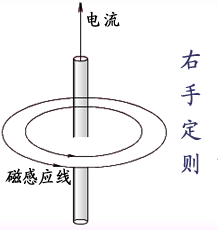| 二、畢奧-薩伐爾定律應用舉例 |
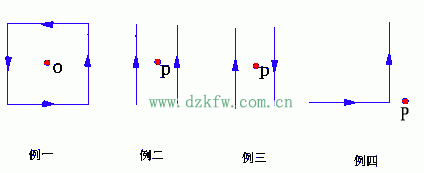
| 兩種基本電流周圍的磁感應強度的分布：載流直導線；圓電流。 例1.載流長直導線的磁場 |
 |
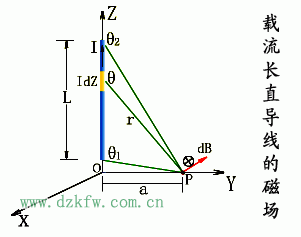解：建立如圖坐標系，在載流直導線上，任取一電流元Idz，由畢-薩定律得元電流在P點產(chǎn)生的磁感應強度大小為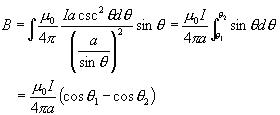： 方向為垂直進入紙面。所有電流元在P點產(chǎn)生的磁場方向相同，所以求總磁感強度的積分為標量積分，即： （1） 由圖得： ,即： 此外： ， 代入（1）可得： 討論：（1）無限長直通電導線的磁場：  （2）半無限長直通電導線的磁場：  （3）其他例子 |
 |
| 例2:圓形載流導線軸線上的磁場：設在真空中，有一半徑為 R ，通電流為 I 的細導線圓環(huán)，求其軸線上距圓心 O 為 x 處的P點的磁感應強度。 解：建立坐標系如圖， |
 |
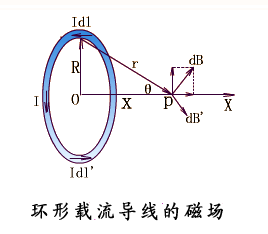任取電流元 ，由畢-薩定律得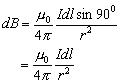： ，方向如圖： ，所有dB形成錐面。將dB進行正交分解：  ，則由由對稱性分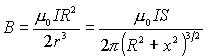析得： ，所以有:  ，因為： ,r=常量，所以：  ，又因為： 所以：   ，方向：沿x軸正方向，與電流成右螺旋關系。討論：（1）圓心處的磁場：x=0 ，  。（2）當 即P點遠離圓環(huán)電流時，P點的磁感應強度為：  。 例3：設有一密繞直螺線管。半徑為 R ，通電流 I。總長度L，總匝數(shù)N（單位長度繞有n 匝線圈），試求管內(nèi)部軸線上一點 P 處的磁感應強度。 |
 |
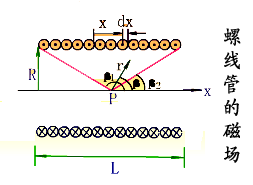解：建立坐標系，在距P 點 x 處任意截取一小段 dx ，其線圈匝數(s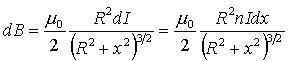hù)為 : 電流為： 。其相當于一個圓電流，它在P點的磁感應強度為： 。因為螺線管各小段在P點的磁感應強度的方向均沿軸線向右，所以整個螺線管在P點的磁感應強度的大小為：  因為：  代入上式得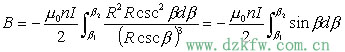：  所以：  討論： （1）管內(nèi)軸線上中點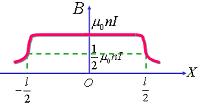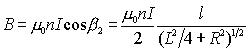的磁場:   （2）當 L>>R時，為無限長螺線管。此時,   ，管內(nèi)磁場 。即無限長螺線管軸線上及內(nèi)部為均勻磁場，方向與軸線平行滿足右手定則。（3）半無限長螺線管左端面（或右端面），此時:  因此：  ，即其端面中心軸線上磁感應強度的大小為管內(nèi)的一半。 |
返回頂部
刷新頁面
下到頁底