磁感應線是套連載閉合載流回路上的閉合線。若取磁感應強線的環路積分,則因B與dL的夾角θ=0,cosθ=1,故在每條線上![]() ,從而
,從而![]() 。安培環路定理就是反映磁感應這一特點的。
。安培環路定理就是反映磁感應這一特點的。
安培環路定理:磁感應強度沿任何閉合環路L的線積分,等于穿過這環路所有電流強度的代數和的μ0倍。用公式表示有:![]() 。
。
其中電流I的正負規定如下:當穿過回路L的電流方向與回路L的環繞方向服從右手法則時,I>0,反之,I<0。如果電流不穿過回路L,則它對上式右端無貢獻。

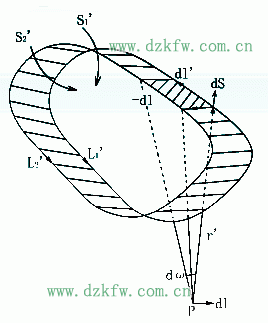
其中![]() 代表dS對場點P所張的立體角dω,沿L'的積分代表整個載流回路作位移-dl時掃過的帶狀面對P點所張的立體角ω。所以
代表dS對場點P所張的立體角dω,沿L'的積分代表整個載流回路作位移-dl時掃過的帶狀面對P點所張的立體角ω。所以![]() 。
。
假設以L'為邊界作一曲面S',S'對P點也張有一定的立體角Ω。當L'平移時,Ω隨之改變。如上圖L2'和L1'分別是L'沿-dl平移前后的新、舊位置,令S2'和S1'代表S'的相應位置,Ω2和Ω1代表相應的立體角。因S2'和S1'和帶狀面組成閉合曲面,它對于外邊的P點所張的總立體角Ω2-Ω1+ω=0,所以:
![]()
由于dl是任意的,從而![]() ,即磁場正比于載流線圈對場點所張立體角的梯度。
,即磁場正比于載流線圈對場點所張立體角的梯度。
假設場點P沿閉合的安培環路L移動一周,則環路積分 將正比于立體角Ω在此過程中的總改變量ΔΩ。如果L不與L'套連,則ΔΩ=0,于是:![]() 但是,當L與L'套連時,ΔΩ=4π。因此:
但是,當L與L'套連時,ΔΩ=4π。因此:![]() 。所以安培環路定理得證。
。所以安培環路定理得證。
注意:該定理表達式中各物理量的意義。I只包括穿過閉合回路L的電流。B代表空間所有電流產生的磁場強度的矢量和,其中也包括那些不穿過L的電流產生的磁場,只不過后者的磁場沿閉合環路積分后的總效果為0。I只包括穿過閉合回路L的電流。


 返回頂部
返回頂部 刷新頁面
刷新頁面 下到頁底
下到頁底